1. 下列运算正确的是(
A.$(m^{2})^{3}=m^{5}$
B.$m^{3}· m^{2}=m^{5}$
C.$(m + n)^{2}=m^{2}+n^{2}$
D.$m^{3}+m^{3}=m^{6}$
B
)A.$(m^{2})^{3}=m^{5}$
B.$m^{3}· m^{2}=m^{5}$
C.$(m + n)^{2}=m^{2}+n^{2}$
D.$m^{3}+m^{3}=m^{6}$
答案:1. B
2. 一种新型病毒的直径约为 0.000023 毫米,用科学记数法表示为(
A.$0.23×10^{-6}$毫米
B.$2.3×10^{6}$毫米
C.$2.3×10^{-5}$毫米
D.$2.3×10^{-4}$毫米
C
)A.$0.23×10^{-6}$毫米
B.$2.3×10^{6}$毫米
C.$2.3×10^{-5}$毫米
D.$2.3×10^{-4}$毫米
答案:2. C
3. 在下列图形中,既是轴对称图形又是中心对称图形的是(

C
)
答案:3. C
4. 有下列命题:①多边形的外角和是$360^{\circ}$;②两条直线被第三条直线所截,内错角相等;③三角形的 3 个内角中,至少有 2 个角是锐角. 其中真命题的个数为(
A.0
B.1
C.2
D.3
C
)A.0
B.1
C.2
D.3
答案:4. C
解析:
①多边形的外角和是$360^{\circ}$,是真命题;
②两条平行直线被第三条直线所截,内错角相等,原命题缺少“平行”条件,是假命题;
③三角形的3个内角中,至少有2个角是锐角,是真命题。
真命题的个数为2。
C
②两条平行直线被第三条直线所截,内错角相等,原命题缺少“平行”条件,是假命题;
③三角形的3个内角中,至少有2个角是锐角,是真命题。
真命题的个数为2。
C
5. 如图,将$△ ABC$绕点 A 顺时针旋转一定的角度得到$△ AB'C'$,使点$B'$恰好落在边 AC 上. 若$AB = 2$,$AC' = 5$,则$B'C$的长为(
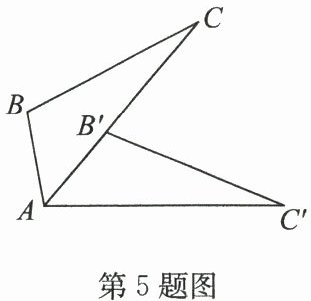
A.2
B.3
C.4
D.5
B
)
A.2
B.3
C.4
D.5
答案:5. B
解析:
解:由旋转性质得,$AC=AC'=5$,$AB'=AB=2$。
因为点$B'$在边$AC$上,所以$B'C=AC - AB'=5 - 2=3$。
答案:B
因为点$B'$在边$AC$上,所以$B'C=AC - AB'=5 - 2=3$。
答案:B
6. 不等式$2 - x < 1$的解集在数轴上表示正确的是(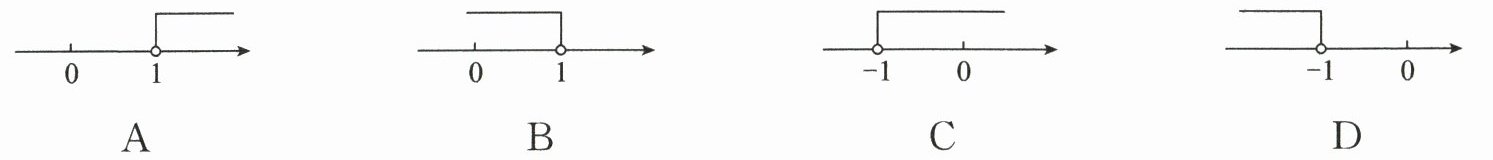
A
)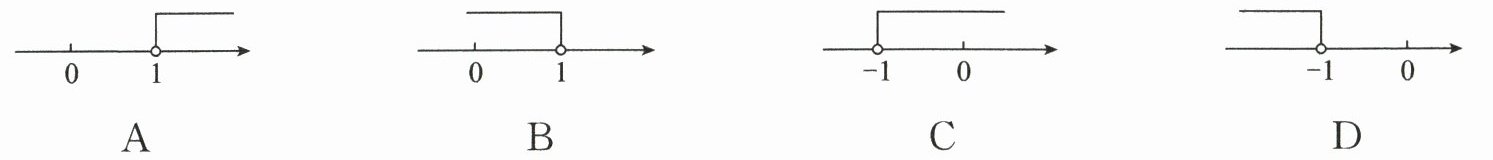
答案:6. A
解析:
解:$2 - x < 1$
$-x < 1 - 2$
$-x < -1$
$x > 1$
在数轴上表示为选项A。
$-x < 1 - 2$
$-x < -1$
$x > 1$
在数轴上表示为选项A。
7. 甲、乙两人练习跑步,如果甲让乙先跑 10 米,那么甲跑 5 秒就能追上乙;如果甲让乙先跑 2 秒,那么甲跑 4 秒就能追上乙. 若甲、乙每秒分别跑$x$米,$y$米,则列出方程组应是(
A.$\begin{cases}5x + 10 = 5y \\ 4x - 4y = 2\end{cases}$
B.$\begin{cases}5x = 5y + 10 \\ 4x - 2 = 4y\end{cases}$
C.$\begin{cases}5x - 5y = 10 \\ 4(x - y) = 2y\end{cases}$
D.$\begin{cases}5(x - y) = 10 \\ 4(x - y) = 2\end{cases}$
C
)A.$\begin{cases}5x + 10 = 5y \\ 4x - 4y = 2\end{cases}$
B.$\begin{cases}5x = 5y + 10 \\ 4x - 2 = 4y\end{cases}$
C.$\begin{cases}5x - 5y = 10 \\ 4(x - y) = 2y\end{cases}$
D.$\begin{cases}5(x - y) = 10 \\ 4(x - y) = 2\end{cases}$
答案:7. C
8. 如图,在$△ ABC$中,$∠ A = 48^{\circ}$,$∠ ABC$与$∠ ACD$的平分线交于点$A_{1}$,得$∠ A_{1}$;$∠ A_{1}BC$与$∠ A_{1}CD$的平分线相交于点$A_{2}$,得$∠ A_{2}$;$······$;$∠ A_{n - 1}BC$与$∠ A_{n - 1}CD$的平分线交于点$A_{n}$,要使$∠ A_{n}$的度数为整数,则$n$的最大值为(
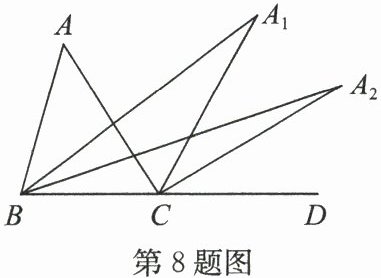
A.2
B.3
C.4
D.5
C
)
A.2
B.3
C.4
D.5
答案:8. C
解析:
解:在$△ ABC$中,$∠ ACD = ∠ A + ∠ ABC$。
因为$BA_1$平分$∠ ABC$,$CA_1$平分$∠ ACD$,所以$∠ A_1BC = \frac{1}{2}∠ ABC$,$∠ A_1CD = \frac{1}{2}∠ ACD$。
$∠ A_1 = ∠ A_1CD - ∠ A_1BC = \frac{1}{2}∠ ACD - \frac{1}{2}∠ ABC = \frac{1}{2}(∠ ACD - ∠ ABC) = \frac{1}{2}∠ A = \frac{48°}{2} = 24°$。
同理,$∠ A_2 = \frac{1}{2}∠ A_1 = \frac{24°}{2} = 12°$,$∠ A_3 = \frac{1}{2}∠ A_2 = 6°$,$∠ A_4 = \frac{1}{2}∠ A_3 = 3°$,$∠ A_5 = \frac{1}{2}∠ A_4 = 1.5°$(非整数)。
要使$∠ A_n$为整数,$n$的最大值为4。
答案:C
因为$BA_1$平分$∠ ABC$,$CA_1$平分$∠ ACD$,所以$∠ A_1BC = \frac{1}{2}∠ ABC$,$∠ A_1CD = \frac{1}{2}∠ ACD$。
$∠ A_1 = ∠ A_1CD - ∠ A_1BC = \frac{1}{2}∠ ACD - \frac{1}{2}∠ ABC = \frac{1}{2}(∠ ACD - ∠ ABC) = \frac{1}{2}∠ A = \frac{48°}{2} = 24°$。
同理,$∠ A_2 = \frac{1}{2}∠ A_1 = \frac{24°}{2} = 12°$,$∠ A_3 = \frac{1}{2}∠ A_2 = 6°$,$∠ A_4 = \frac{1}{2}∠ A_3 = 3°$,$∠ A_5 = \frac{1}{2}∠ A_4 = 1.5°$(非整数)。
要使$∠ A_n$为整数,$n$的最大值为4。
答案:C