新知梳理
成轴对称的两个图形中,不在对称轴上的两个对应点的连线段被对称轴
成轴对称的两个图形中,不在对称轴上的两个对应点的连线段被对称轴
垂直平分
.也就是说,成轴对称的两个图形中,对称轴是任意两个对称点连线段的垂直平分线
.答案:垂直平分 垂直平分线
1.(2024·江宁区月考)下列图形中,点 A 与点 B 关于直线 l 对称的是(
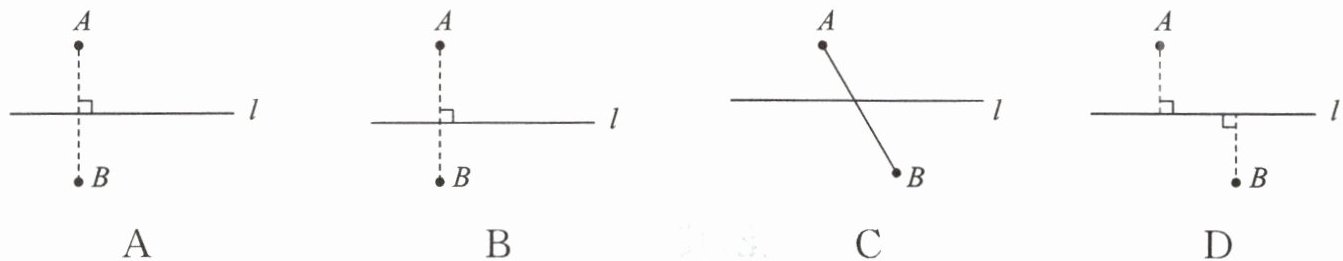
A
)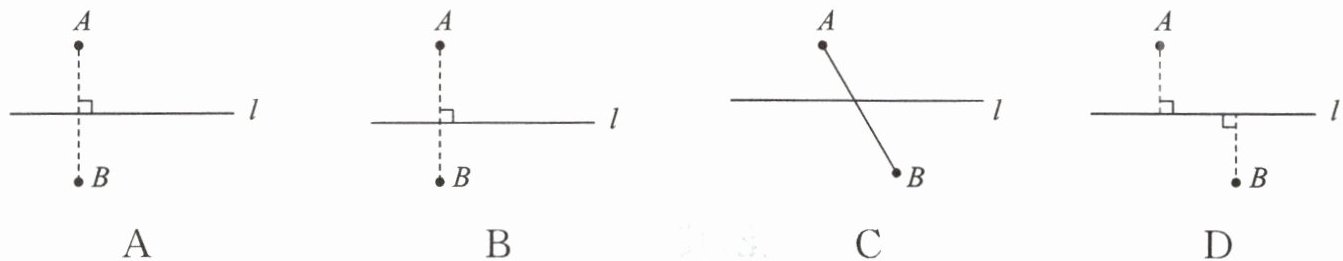
答案:1. A
2. 如图,线段 AB 和 $ A'B' $ 关于直线 MN 对称,则 $ AA' ⊥ $
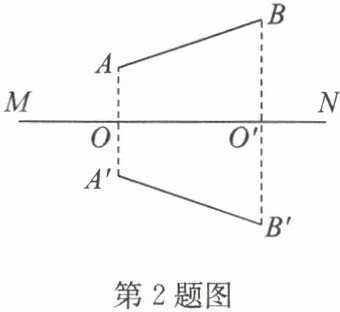
MN
,$ BB' ⊥ $MN
,$ OA = $OA'
,$ O'B = $O'B'
.
答案:2. MN MN OA' O'B'
解析:
MN;MN;OA';O'B'
3. 如图,已知 $ △ ABC $ 和直线 l,作出 $ △ ABC $ 关于直线 l 的对称图形.
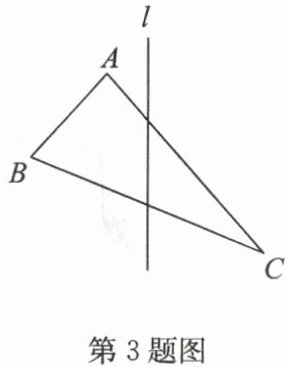

答案:
3. 解:如答图,△A'B'C' 即为所求。
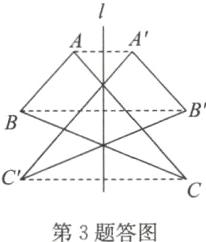
3. 解:如答图,△A'B'C' 即为所求。

4. 如图,四边形 ABCD 与四边形 EFGH 关于直线 MN 对称.
(1)线段 AD 的对称线段是
(2)AE 与 BF 平行吗?为什么?
(3)若 AE 与 BF 平行,则能说明轴对称图形中对称点的连线一定互相平行吗?
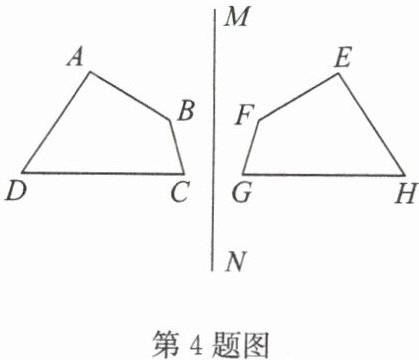
(1)线段 AD 的对称线段是
EH
,$ CD = $GH
,$ ∠ CBA = $∠GFE
,$ ∠ ADC = $∠EHG
.(2)AE 与 BF 平行吗?为什么?
(3)若 AE 与 BF 平行,则能说明轴对称图形中对称点的连线一定互相平行吗?

答案:4. (1) EH GH ∠GFE ∠EHG
(2) 解:AE//BF. 理由如下:
因为每对对称点的连线段都被对称轴垂直平分,
即 AE⊥MN,BF⊥MN,所以 AE//BF.
(3) AE//BF 不一定能说明对称点的连线一定互相平行,还有可能共线。
(2) 解:AE//BF. 理由如下:
因为每对对称点的连线段都被对称轴垂直平分,
即 AE⊥MN,BF⊥MN,所以 AE//BF.
(3) AE//BF 不一定能说明对称点的连线一定互相平行,还有可能共线。