新知梳理
1.
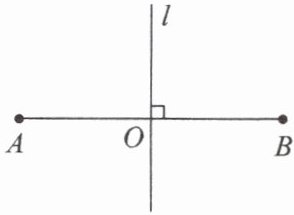
2. 如图,如果直线 $ l $ 是线段 $ AB $ 的垂直平分线,$ O $ 为垂足,那么线段 $ OA $ 与 $ OB $ 关于 $ l $ 成
1.
垂直且平分
一条线段的直线叫作这条线段的垂直平分线,简称中垂线
.2. 如图,如果直线 $ l $ 是线段 $ AB $ 的垂直平分线,$ O $ 为垂足,那么线段 $ OA $ 与 $ OB $ 关于 $ l $ 成
轴对称
,$ A $,$ B $ 为对称点
,点 $ O $ 的对称点是其自身.
答案:1.垂直且平分 中垂线 2.轴对称 对称点
1. 关于线段的垂直平分线,给出下列说法:①一条线段与其垂直平分线的交点是这条线段的中点;②线段的垂直平分线是一条直线;③线段垂直于它的垂直平分线;④线段的垂直平分线是它的对称轴.其中正确的有(
A.1 个
B.2 个
C.3 个
D.4 个
D
)A.1 个
B.2 个
C.3 个
D.4 个
答案:1.D
解析:
①一条线段与其垂直平分线的交点是这条线段的中点,正确;
②线段的垂直平分线是一条直线,正确;
③线段垂直于它的垂直平分线,正确;
④线段的垂直平分线是它的对称轴,正确。
正确的有4个。
D
②线段的垂直平分线是一条直线,正确;
③线段垂直于它的垂直平分线,正确;
④线段的垂直平分线是它的对称轴,正确。
正确的有4个。
D
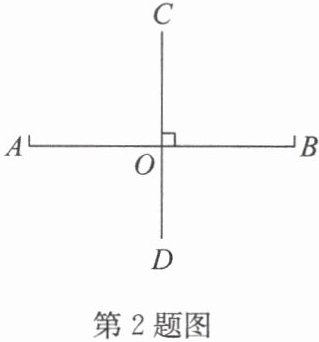
2. 如图,如果直线 $ CD $ 是线段 $ AB $ 的垂直平分线,垂足为 $ O $,且 $ AO = 2 $,那么 $ AB = $
4
.
答案:2.4
解析:
解:因为直线 $ CD $ 是线段 $ AB $ 的垂直平分线,垂足为 $ O $,所以 $ AO = BO $。已知 $ AO = 2 $,则 $ BO = 2 $,因此 $ AB = AO + BO = 2 + 2 = 4 $。
4
4
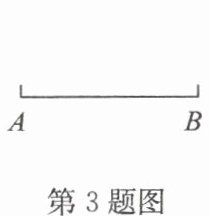
3. 作图:如图,用尺规作线段 $ AB $ 的垂直平分线.

答案:
3.解:如答图,直线MN即为所求.
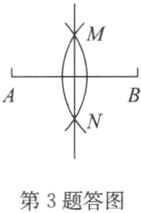
3.解:如答图,直线MN即为所求.

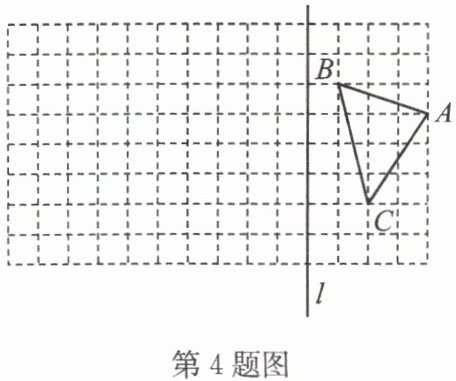
4. 如图,在由边长为 1 个单位长度的小正方形组成的 $ 8×14 $ 网格中,$ △ ABC $ 的顶点都在格点上,直线 $ l $ 与网格线重合.
(1) 以直线 $ l $ 为对称轴,画出 $ △ ABC $ 关于直线 $ l $ 对称的 $ △ A_1B_1C_1 $;
(2) 画出将 $ △ ABC $ 向左平移 11 个单位长度,再向下平移 1 个单位长度,得到的 $ △ A_2B_2C_2 $;
(3) 选择两个网格点,利用直尺画出线段 $ A_1A_2 $ 的垂直平分线.(保留作图痕迹)
(1) 以直线 $ l $ 为对称轴,画出 $ △ ABC $ 关于直线 $ l $ 对称的 $ △ A_1B_1C_1 $;
(2) 画出将 $ △ ABC $ 向左平移 11 个单位长度,再向下平移 1 个单位长度,得到的 $ △ A_2B_2C_2 $;
(3) 选择两个网格点,利用直尺画出线段 $ A_1A_2 $ 的垂直平分线.(保留作图痕迹)

答案:
4.解:(1)如答图,△A₁B₁C₁即为所求,

(2)如答图,△A₂B₂C₂即为所求.
(3)如答图,直线DE即为所求.
4.解:(1)如答图,△A₁B₁C₁即为所求,

(2)如答图,△A₂B₂C₂即为所求.
(3)如答图,直线DE即为所求.