新知梳理
1. 一般地,将一个平面图形沿
2. 成轴对称的两个图形可以
1. 一般地,将一个平面图形沿
某条直线
翻折后得到另一个图形的平面变换叫作轴对称
,这条直线叫作对称轴
,此时称这两个图形成轴对称
。2. 成轴对称的两个图形可以
重合
,对应线段相等
,对应角也相等
。答案:1.某条直线 轴对称 对称轴 成轴对称
2.重合 相等 相等
2.重合 相等 相等
1. 下列各选项中,两个三角形成轴对称的是(
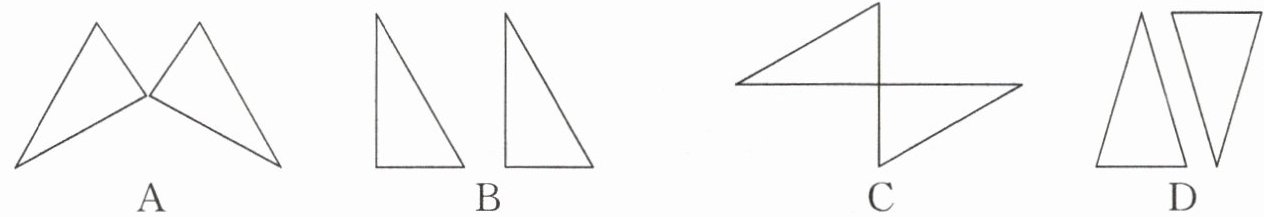
A
)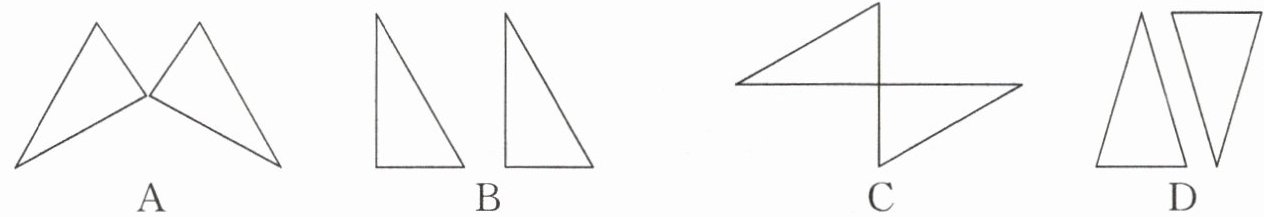
答案:1.A
2. 如图,$△ ABC$与$△ DEF$关于直线$MN$成轴对称,那么线段$AC$的对应线段是(
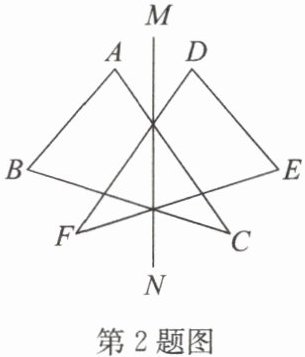
A.$AB$
B.$DF$
C.$DE$
D.$EF$
B
)
A.$AB$
B.$DF$
C.$DE$
D.$EF$
答案:2.B
解析:
证明:
∵△ABC与△DEF关于直线MN成轴对称,
∴点A的对应点是点D,点C的对应点是点F,
∴线段AC的对应线段是DF。
答案:B
∵△ABC与△DEF关于直线MN成轴对称,
∴点A的对应点是点D,点C的对应点是点F,
∴线段AC的对应线段是DF。
答案:B
3. 如图,$△ ABC$与$△ DEF$关于直线$l$对称,若$∠ A = 60^{\circ}$,$∠ B = 80^{\circ}$,则$∠ F =$
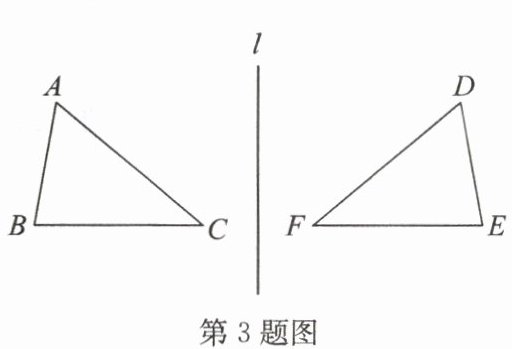
40°
。
答案:3.40°
解析:
证明:在$△ ABC$中,$∠ A = 60^{\circ}$,$∠ B = 80^{\circ}$,根据三角形内角和定理,$∠ C=180^{\circ}-∠ A-∠ B=180^{\circ}-60^{\circ}-80^{\circ}=40^{\circ}$。
因为$△ ABC$与$△ DEF$关于直线$l$对称,所以$△ ABC≌△ DEF$,则$∠ F = ∠ C = 40^{\circ}$。
$40^{\circ}$
因为$△ ABC$与$△ DEF$关于直线$l$对称,所以$△ ABC≌△ DEF$,则$∠ F = ∠ C = 40^{\circ}$。
$40^{\circ}$
4. 从汽车后视镜中看见某车牌后$5$位号码是 ,该号码实际是
,该号码实际是
 ,该号码实际是
,该号码实际是BA629
。答案:4.BA629
5. 如图,由边长均为$1$的小正方形组成的网格图中,点$A$,$B$,$C$都在格点(正方形的顶点)上。
(1)$△ ABC$的面积等于
(2)画出$△ ABC$关于直线$l$的对称图形。
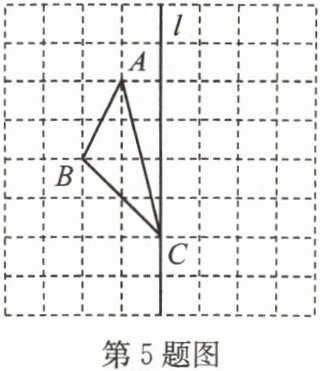
(1)$△ ABC$的面积等于
3
;(2)画出$△ ABC$关于直线$l$的对称图形。

答案:
5.(1)3
(2)解:如答图,△A₁B₁C即为所求,
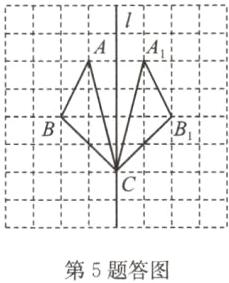
5.(1)3
(2)解:如答图,△A₁B₁C即为所求,
