1. 如图,D 是$△ ABC$内一点.
求证:$△ ABD,△ BDC,△ ADC$不可能都是锐角三角形.
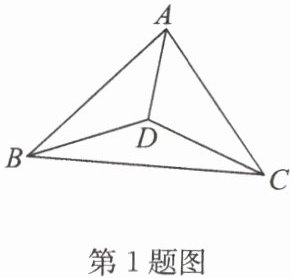
求证:$△ ABD,△ BDC,△ ADC$不可能都是锐角三角形.

答案:1.证明:假设△ABD,△BDC,△ADC都是锐角三角形,则∠ADB,∠BDC,∠ADC都是锐角,
所以∠ADB+∠BDC+∠ADC<270°,
这与∠ADB+∠BDC+∠ADC=360°(周角为360°)相矛盾,
所以假设不成立,
所以△ABD,△BDC,△ADC不可能都是锐角三角形。
所以∠ADB+∠BDC+∠ADC<270°,
这与∠ADB+∠BDC+∠ADC=360°(周角为360°)相矛盾,
所以假设不成立,
所以△ABD,△BDC,△ADC不可能都是锐角三角形。
2. 用反证法证明:两直线平行,同旁内角互补.
答案:
2.解:已知:如答图,直线l₁ // l₂,l₁和l₂被l₃所截。
求证:∠1+∠2=180°.

证明:假设∠1+∠2≠180°.
因为l₁//l₂(已知),
所以∠1=∠3(两直线平行,同位角相等).
因为∠1+∠2≠180°,
所以∠2+∠3≠180°,这与∠2+∠3=180°(平角为180°)相矛盾,
所以假设不成立,所以∠1+∠2=180°.
2.解:已知:如答图,直线l₁ // l₂,l₁和l₂被l₃所截。
求证:∠1+∠2=180°.

证明:假设∠1+∠2≠180°.
因为l₁//l₂(已知),
所以∠1=∠3(两直线平行,同位角相等).
因为∠1+∠2≠180°,
所以∠2+∠3≠180°,这与∠2+∠3=180°(平角为180°)相矛盾,
所以假设不成立,所以∠1+∠2=180°.
3. 求证:$x^{2}=2$中x不是有理数.
答案:3.证明:假设x是有理数,则x可以表示为$\frac{a}{b}$(a,b均为整数且互质).
因为x²=2,所以$(\frac{a}{b})^2$=2,即$\frac{a^2}{b^2}$=2,所以a² = 2b².因为2b²是偶数,所以a²是偶数,所以a是偶数.
设a=2c(c为整数),则4c²=a²=2b²,
所以b²=2c²,所以b也是偶数,这与a,b互质相矛盾,所以假设不成立,所以x²=2中x不是有理数.
因为x²=2,所以$(\frac{a}{b})^2$=2,即$\frac{a^2}{b^2}$=2,所以a² = 2b².因为2b²是偶数,所以a²是偶数,所以a是偶数.
设a=2c(c为整数),则4c²=a²=2b²,
所以b²=2c²,所以b也是偶数,这与a,b互质相矛盾,所以假设不成立,所以x²=2中x不是有理数.