1. 如图,线段 OA 与射线 OB 垂直,P 是射线 OB 上一动点(与点 O 不重合),∠OAP 的平分线与∠APO 的平分线交于点 E,与△APO 的外角∠OPD 的平分线交于点 F.
(1)求∠AEP 的度数;
(2)当点 P 在射线 OB 上运动时,△EPF 的形状是否变化?若变化,请写出它的变化规律;若不变,请写出它的形状,并说明理由.
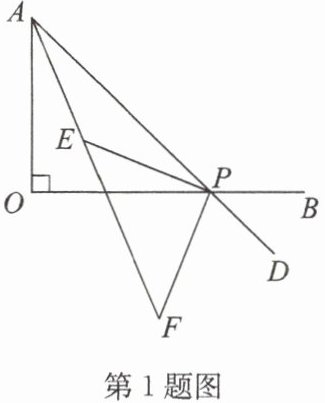
(1)求∠AEP 的度数;
(2)当点 P 在射线 OB 上运动时,△EPF 的形状是否变化?若变化,请写出它的变化规律;若不变,请写出它的形状,并说明理由.

答案:1.解:(1)因为OA⊥OB,所以∠AOB = 90°,
所以∠OAP + ∠OPA = 90°.
因为AE,PE分别平分∠OAP,∠OPA,
所以∠EAP = $\frac{1}{2}$∠OAP,∠EPA = $\frac{1}{2}$∠OPA,
所以∠EAP + ∠EPA = $\frac{1}{2}$∠OAP + $\frac{1}{2}$∠OPA = $\frac{1}{2}$(∠OAP + ∠OPA) = $\frac{1}{2}$×90° = 45°,
所以∠AEP = 180° - (∠EAP + ∠EPA) = 180° - 45° = 135°.
(2)△EPF是等腰直角三角形,理由如下:
因为PF平分∠OPD,所以∠OPF = $\frac{1}{2}$∠OPD.
因为∠APO + ∠OPD = 180°,
所以∠EPO + ∠OPF = $\frac{1}{2}$∠APO + $\frac{1}{2}$∠OPD = $\frac{1}{2}$(∠APO + ∠OPD) = $\frac{1}{2}$×180° = 90°,
所以△EPF是直角三角形.
又因为∠PEF = 180° - ∠AEP = 180° - 135° = 45°,所以△EPF是等腰直角三角形.
所以∠OAP + ∠OPA = 90°.
因为AE,PE分别平分∠OAP,∠OPA,
所以∠EAP = $\frac{1}{2}$∠OAP,∠EPA = $\frac{1}{2}$∠OPA,
所以∠EAP + ∠EPA = $\frac{1}{2}$∠OAP + $\frac{1}{2}$∠OPA = $\frac{1}{2}$(∠OAP + ∠OPA) = $\frac{1}{2}$×90° = 45°,
所以∠AEP = 180° - (∠EAP + ∠EPA) = 180° - 45° = 135°.
(2)△EPF是等腰直角三角形,理由如下:
因为PF平分∠OPD,所以∠OPF = $\frac{1}{2}$∠OPD.
因为∠APO + ∠OPD = 180°,
所以∠EPO + ∠OPF = $\frac{1}{2}$∠APO + $\frac{1}{2}$∠OPD = $\frac{1}{2}$(∠APO + ∠OPD) = $\frac{1}{2}$×180° = 90°,
所以△EPF是直角三角形.
又因为∠PEF = 180° - ∠AEP = 180° - 135° = 45°,所以△EPF是等腰直角三角形.
2. 三角形内角和定理告诉我们:三角形三个内角的和等于 180°.
【定理推论】(1)如图①,在△ABC 中,有∠A+∠B+∠ACB=180°,D 是 BC 延长线上一点,由平角的定义可得∠ACD+∠ACB=180°,所以∠ACD=
【初步运用】(2)如图②,D,E 分别是△ABC 的边 AB,AC 延长线上的点.
①若∠A=80°,∠DBC=150°,则∠ACB=
②若∠A=80°,则∠DBC+∠ECB=
【拓展延伸】(3)如图③,D,E 分别是四边形 ABPC 的边 AB,AC 延长线上的点.
①若∠A=80°,∠P=150°,则∠DBP+∠ECP=
②分别作∠DBP 和∠ECP 的平分线,交于点 O,如图④. 若∠O=50°,则∠A 和∠BPC 的数量关系为
③分别作∠DBP 和∠ECP 的平分线 BM,CN,如图⑤. 若∠A=∠P,求证:BM//CN.
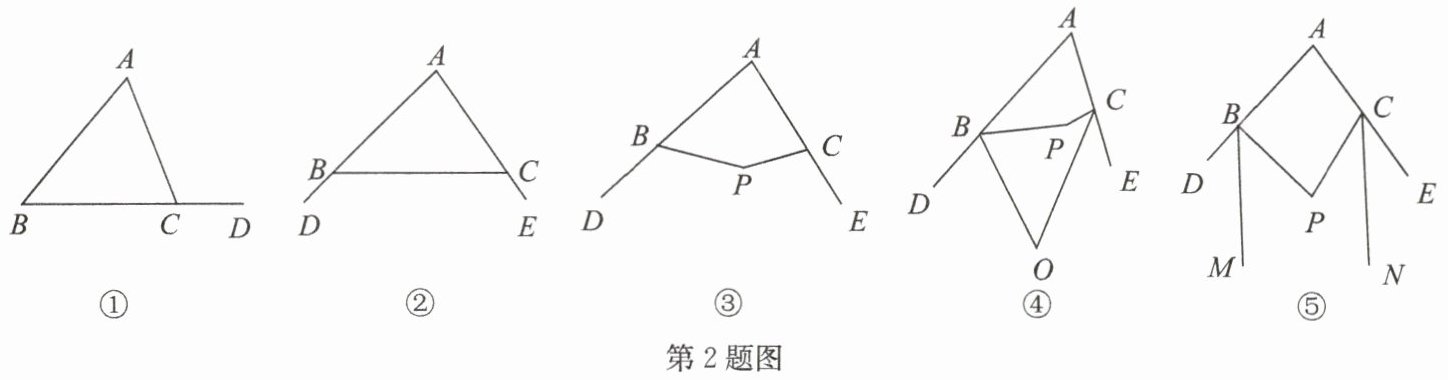
【定理推论】(1)如图①,在△ABC 中,有∠A+∠B+∠ACB=180°,D 是 BC 延长线上一点,由平角的定义可得∠ACD+∠ACB=180°,所以∠ACD=
∠A + ∠B
. 从而得到三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.【初步运用】(2)如图②,D,E 分别是△ABC 的边 AB,AC 延长线上的点.
①若∠A=80°,∠DBC=150°,则∠ACB=
70°
;②若∠A=80°,则∠DBC+∠ECB=
260°
.【拓展延伸】(3)如图③,D,E 分别是四边形 ABPC 的边 AB,AC 延长线上的点.
①若∠A=80°,∠P=150°,则∠DBP+∠ECP=
230°
;②分别作∠DBP 和∠ECP 的平分线,交于点 O,如图④. 若∠O=50°,则∠A 和∠BPC 的数量关系为
∠BPC = ∠A + 100°
;③分别作∠DBP 和∠ECP 的平分线 BM,CN,如图⑤. 若∠A=∠P,求证:BM//CN.

答案:
2.(1)∠A + ∠B
(2)①70°②260°
(3)①230°
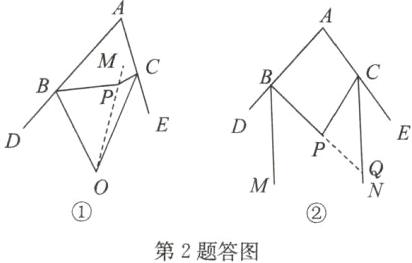
②∠BPC = ∠A + 100° 点拨:如答图①,连接OP并延长至点M,由三角形外角的性质可得∠MPB = ∠OBP + ∠BOP,∠MPC = ∠PCO + ∠POC,所以∠MPB + ∠MPC = ∠PBO + ∠PCO + ∠POB + ∠POC,即∠BPC = ∠BOC + ∠OBP + ∠OCP.因为BO,CO分别平分∠PBD,∠PCE,所以∠PBO = $\frac{1}{2}$∠PBD,∠PCO = $\frac{1}{2}$∠PCE.因为∠BOC = 50°,所以∠BPC = ∠BOC + ∠OBP + ∠OCP = 50° + $\frac{1}{2}$(∠PBD + ∠PCE) = 50° + $\frac{1}{2}$[360° - (∠ABP + ∠ACP)].又由四边形内角和为360°,得∠ABP + ∠ACP = 360° - (∠A + ∠BPC),所以∠BPC = 50° + $\frac{1}{2}$(∠A + ∠BPC),所以∠BPC = ∠A + 100°.
③证明:如答图②,延长BP交CN于点Q,
因为BM平分∠DBP,CN平分∠ECP,
所以∠DBP = 2∠MBP,∠ECP = 2∠NCP.
因为∠DBP + ∠ECP = ∠A + ∠BPC,∠A = ∠BPC,所以2∠MBP + 2∠NCP = ∠A + ∠BPC = 2∠BPC,所以∠BPC = ∠MBP + ∠NCP.
因为∠BPC = ∠PQC + ∠NCP,
所以∠MBP = ∠PQC,
所以BM//CN.
2.(1)∠A + ∠B
(2)①70°②260°
(3)①230°
②∠BPC = ∠A + 100° 点拨:如答图①,连接OP并延长至点M,由三角形外角的性质可得∠MPB = ∠OBP + ∠BOP,∠MPC = ∠PCO + ∠POC,所以∠MPB + ∠MPC = ∠PBO + ∠PCO + ∠POB + ∠POC,即∠BPC = ∠BOC + ∠OBP + ∠OCP.因为BO,CO分别平分∠PBD,∠PCE,所以∠PBO = $\frac{1}{2}$∠PBD,∠PCO = $\frac{1}{2}$∠PCE.因为∠BOC = 50°,所以∠BPC = ∠BOC + ∠OBP + ∠OCP = 50° + $\frac{1}{2}$(∠PBD + ∠PCE) = 50° + $\frac{1}{2}$[360° - (∠ABP + ∠ACP)].又由四边形内角和为360°,得∠ABP + ∠ACP = 360° - (∠A + ∠BPC),所以∠BPC = 50° + $\frac{1}{2}$(∠A + ∠BPC),所以∠BPC = ∠A + 100°.
③证明:如答图②,延长BP交CN于点Q,
因为BM平分∠DBP,CN平分∠ECP,
所以∠DBP = 2∠MBP,∠ECP = 2∠NCP.
因为∠DBP + ∠ECP = ∠A + ∠BPC,∠A = ∠BPC,所以2∠MBP + 2∠NCP = ∠A + ∠BPC = 2∠BPC,所以∠BPC = ∠MBP + ∠NCP.
因为∠BPC = ∠PQC + ∠NCP,
所以∠MBP = ∠PQC,
所以BM//CN.
