1. 观察下列等式:①$2×4 - 3 = 1×5$;②$3×5 - 3 = 2×6$;③$4×6 - 3 = 3×7$.
(1) 第④个等式为
(2) 写出第$n$个等式,并验证其正确性.
(1) 第④个等式为
$ 5×7 - 3 = 4×8 $
;(2) 写出第$n$个等式,并验证其正确性.
答案:1. (1) $ 5×7 - 3 = 4×8 $
(2) 解:第ⓝ个等式为 $ (n + 1)(n + 3) - 3 = n(n + 4) $。
证明:因为左边 $ = n^{2} + 4n + 3 - 3 = n^{2} + 4n $,
右边 $ = n^{2} + 4n $,所以左边 $ = $ 右边,
所以等式成立。
(2) 解:第ⓝ个等式为 $ (n + 1)(n + 3) - 3 = n(n + 4) $。
证明:因为左边 $ = n^{2} + 4n + 3 - 3 = n^{2} + 4n $,
右边 $ = n^{2} + 4n $,所以左边 $ = $ 右边,
所以等式成立。
2. 先阅读材料,再解答问题.
已知$x^{2} - 2x + y^{2} + 6y + 10 = 0$,求$x$,$y$的值.
解:$x^{2} - 2x + y^{2} + 6y + 10 = x^{2} - 2x + 1 + y^{2} + 6y + 9 = (x - 1)^{2} + (y + 3)^{2} = 0$.
$\because (x - 1)^{2} ≥ 0$,$(y + 3)^{2} ≥ 0$,$\therefore x - 1 = 0$,$y + 3 = 0$,$\therefore x = 1$,$y = - 3$.
像这样将代数式进行恒等变形,使代数式中出现完全平方式的方法叫作“配方法”.
(1) 已知$a^{2} + b^{2} + 8a - 6b + 25 = 0$,则$a =$
(2) 已知$A = 2x^{2} - 2x - 3$,$B = x^{2} - x - 4$.
①猜想:$A$
②证明猜想成立.
已知$x^{2} - 2x + y^{2} + 6y + 10 = 0$,求$x$,$y$的值.
解:$x^{2} - 2x + y^{2} + 6y + 10 = x^{2} - 2x + 1 + y^{2} + 6y + 9 = (x - 1)^{2} + (y + 3)^{2} = 0$.
$\because (x - 1)^{2} ≥ 0$,$(y + 3)^{2} ≥ 0$,$\therefore x - 1 = 0$,$y + 3 = 0$,$\therefore x = 1$,$y = - 3$.
像这样将代数式进行恒等变形,使代数式中出现完全平方式的方法叫作“配方法”.
(1) 已知$a^{2} + b^{2} + 8a - 6b + 25 = 0$,则$a =$
$ -4 $
,$b =$$ 3 $
.(2) 已知$A = 2x^{2} - 2x - 3$,$B = x^{2} - x - 4$.
①猜想:$A$
$ > $
$B$;(填“$>$”“$<$”或“$=$”)②证明猜想成立.
答案:2. (1) $ -4 $ $ 3 $ 点拨:因为 $ a^{2} + b^{2} + 8a - 6b + 25 = a^{2} + 8a + 16 + b^{2} - 6b + 9 = (a + 4)^{2} + (b - 3)^{2} = 0 $,所以 $ a + 4 = 0 $ 且 $ b - 3 = 0 $,所以 $ a = -4 $,$ b = 3 $。
(2) ① $ > $
② 证明:$ A - B = (2x^{2} - 2x - 3) - (x^{2} - x - 4) = 2x^{2} - 2x - 3 - x^{2} + x + 4 = x^{2} - x + 1 = x^{2} - x + \frac{1}{4} + \frac{3}{4} = (x - \frac{1}{2})^{2} + \frac{3}{4} $。
因为 $ (x - \frac{1}{2})^{2} ≥ 0 $,所以 $ (x - \frac{1}{2})^{2} + \frac{3}{4} > 0 $,
所以 $ A - B > 0 $,所以 $ A > B $。
(2) ① $ > $
② 证明:$ A - B = (2x^{2} - 2x - 3) - (x^{2} - x - 4) = 2x^{2} - 2x - 3 - x^{2} + x + 4 = x^{2} - x + 1 = x^{2} - x + \frac{1}{4} + \frac{3}{4} = (x - \frac{1}{2})^{2} + \frac{3}{4} $。
因为 $ (x - \frac{1}{2})^{2} ≥ 0 $,所以 $ (x - \frac{1}{2})^{2} + \frac{3}{4} > 0 $,
所以 $ A - B > 0 $,所以 $ A > B $。
3. 如图,在$△ ABC$中,$CD ⊥ AB$于点$D$,$G$是$BC$上一点,过点$G$作$GF ⊥ AB$于点$F$,且满足$∠ B = ∠ ADE$. 求证:$∠ CDE = ∠ BGF$.
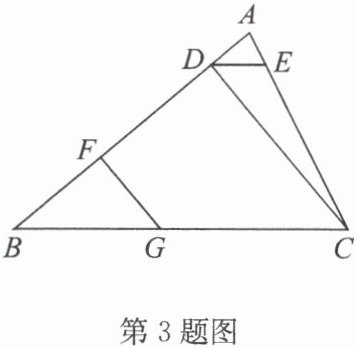

答案:3. 证明:因为 $ CD ⊥ AB $,$ GF ⊥ AB $,
所以 $ ∠ BFG = ∠ BDC = 90^{\circ} $,
所以 $ FG // CD $,所以 $ ∠ BGF = ∠ BCD $。
因为 $ ∠ B = ∠ ADE $,所以 $ DE // BC $,
所以 $ ∠ CDE = ∠ BCD $,所以 $ ∠ CDE = ∠ BGF $。
所以 $ ∠ BFG = ∠ BDC = 90^{\circ} $,
所以 $ FG // CD $,所以 $ ∠ BGF = ∠ BCD $。
因为 $ ∠ B = ∠ ADE $,所以 $ DE // BC $,
所以 $ ∠ CDE = ∠ BCD $,所以 $ ∠ CDE = ∠ BGF $。