1. 已知下列命题:①四边形是多边形;②对顶角相等;③两直线平行,内错角相等;④如果$ab = 0$,那么$a = 0$,$b = 0$;⑤有两个内角互余的三角形是直角三角形;⑥在任何一个直角三角形中,都没有钝角. 其中原命题和逆命题均为真命题的个数为(
A.1
B.2
C.3
D.4
B
)A.1
B.2
C.3
D.4
答案:1.B
解析:
①原命题:四边形是多边形,真;逆命题:多边形是四边形,假。
②原命题:对顶角相等,真;逆命题:相等的角是对顶角,假。
③原命题:两直线平行,内错角相等,真;逆命题:内错角相等,两直线平行,真。
④原命题:如果$ab = 0$,那么$a = 0$,$b = 0$,假;逆命题:如果$a = 0$,$b = 0$,那么$ab = 0$,真。
⑤原命题:有两个内角互余的三角形是直角三角形,真;逆命题:直角三角形有两个内角互余,真。
⑥原命题:在任何一个直角三角形中,都没有钝角,真;逆命题:没有钝角的三角形是直角三角形,假。
原命题和逆命题均为真命题的是③⑤,共2个。
B
②原命题:对顶角相等,真;逆命题:相等的角是对顶角,假。
③原命题:两直线平行,内错角相等,真;逆命题:内错角相等,两直线平行,真。
④原命题:如果$ab = 0$,那么$a = 0$,$b = 0$,假;逆命题:如果$a = 0$,$b = 0$,那么$ab = 0$,真。
⑤原命题:有两个内角互余的三角形是直角三角形,真;逆命题:直角三角形有两个内角互余,真。
⑥原命题:在任何一个直角三角形中,都没有钝角,真;逆命题:没有钝角的三角形是直角三角形,假。
原命题和逆命题均为真命题的是③⑤,共2个。
B
2. 下列命题:①过一点有且只有一条直线与已知直线平行;②如果两条直线被第三条直线所截,那么同位角相等;③相等的两个角是对顶角;④平行于同一直线的两直线互相平行;⑤若两条直线都垂直于同一条直线,则这两条直线互相平行. 其中假命题有(
A.2 个
B.3 个
C.4 个
D.5 个
C
)A.2 个
B.3 个
C.4 个
D.5 个
答案:2.C
解析:
①假命题,过直线外一点有且只有一条直线与已知直线平行;②假命题,两条平行直线被第三条直线所截,同位角相等;③假命题,对顶角相等,但相等的角不一定是对顶角;④真命题;⑤假命题,在同一平面内,若两条直线都垂直于同一条直线,则这两条直线互相平行。假命题有①②③⑤,共4个。
C
C
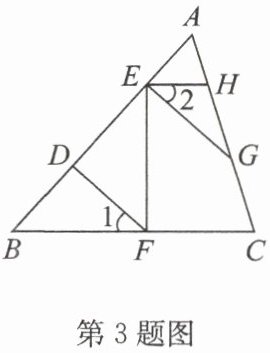
3. 如图,在$△ ABC$中,$D$,$E$是$AB$上的点,$F$是$BC$上一点,$G$,$H$是$AC$上的点,$FD⊥ AB$. 连接$EF$,$EH$,$EG$. 有下列三个选项:①$EG⊥ AB$;②$∠ 1=∠ 2$;③$EH// BC$.
(1)请从三个选项中任选两个与题干结合作为条件,另一个作为结论,写出所有命题,并判断这些命题是真命题还是假命题;
(2)请你选择(1)中的一个真命题,说明理由.
(1)请从三个选项中任选两个与题干结合作为条件,另一个作为结论,写出所有命题,并判断这些命题是真命题还是假命题;
(2)请你选择(1)中的一个真命题,说明理由.

答案:
3.解:(1)有三个命题:①②⇒③,①③⇒②,②③⇒①,它们都是真命题.
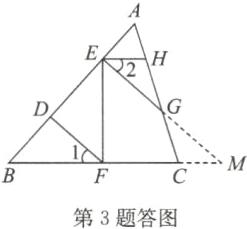
(2)选①②⇒③,理由如下:
如答图,延长EG,BC相交于点M.
因为FD⊥AB,EG⊥AB(已知),
所以∠FDB=∠MEB=90°(垂直定义),
所以DF//EM(同位角相等,两直线平行),
所以∠1=∠M(两直线平行,同位角相等),
因为∠1=∠2(已知),
所以∠M=∠2(等量代换),
所以EH//BC(内错角相等,两直线平行).
3.解:(1)有三个命题:①②⇒③,①③⇒②,②③⇒①,它们都是真命题.
(2)选①②⇒③,理由如下:
如答图,延长EG,BC相交于点M.
因为FD⊥AB,EG⊥AB(已知),
所以∠FDB=∠MEB=90°(垂直定义),
所以DF//EM(同位角相等,两直线平行),
所以∠1=∠M(两直线平行,同位角相等),
因为∠1=∠2(已知),
所以∠M=∠2(等量代换),
所以EH//BC(内错角相等,两直线平行).
