1. 解下列不等式:
(1)$ 5 x - 5 < 2 ( 2 + x ) $;
(2)$ \frac { 2 x - 1 } { 4 } - \frac { 5 x + 2 } { 6 } > - 1 $.
(1)$ 5 x - 5 < 2 ( 2 + x ) $;
(2)$ \frac { 2 x - 1 } { 4 } - \frac { 5 x + 2 } { 6 } > - 1 $.
答案:1.解:(1)去括号,得5x−5<4+2x,
移项,得5x−2x<4+5,
合并同类项,得3x<9,
两边都除以3,得x<3.
(2)去分母,得3(2x−1)−2(5x+2)>−12,
去括号,得6x−3−10x−4>−12,
移项、合并同类项,得−4x>−5,
两边都除以−4,得x<$\frac{5}{4}$.
移项,得5x−2x<4+5,
合并同类项,得3x<9,
两边都除以3,得x<3.
(2)去分母,得3(2x−1)−2(5x+2)>−12,
去括号,得6x−3−10x−4>−12,
移项、合并同类项,得−4x>−5,
两边都除以−4,得x<$\frac{5}{4}$.
2. 解下列不等式,并把解集在数轴上表示出来:
(1)$ \frac { 2 x + 1 } { 3 } - 1 > \frac { 1 - x } { 2 } $;
(2)$ \frac { 2 x } { 3 } - \frac { x + 3 } { 6 } ≥ 1 $;
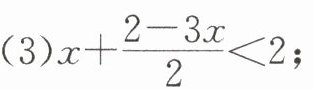
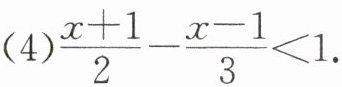
(3)$ x + \frac { 2 - 3 x } { 2 } < 2 $;
(4)$ \frac { x + 1 } { 2 } - \frac { x - 1 } { 3 } < 1 $.
(1)$ \frac { 2 x + 1 } { 3 } - 1 > \frac { 1 - x } { 2 } $;
(2)$ \frac { 2 x } { 3 } - \frac { x + 3 } { 6 } ≥ 1 $;
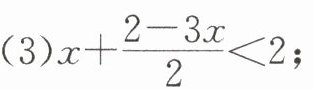
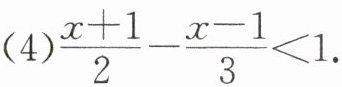
(3)$ x + \frac { 2 - 3 x } { 2 } < 2 $;
(4)$ \frac { x + 1 } { 2 } - \frac { x - 1 } { 3 } < 1 $.
答案:
2.解:(1)去分母,得2(2x+1)−6>3(1−x),
去括号,得4x+2−6>3−3x,
移项、合并同类项,得7x>7,
两边都除以7,得x>1.
解集在数轴上表示如答图①所示.

(2)去分母,得4x−(x+3)≥6,
去括号,得4x−x−3≥6,
移项、合并同类项,得3x≥9,
两边都除以3,得x≥3.
解集在数轴上表示如答图②所示,

(3)去分母,得2x+2−3x<4,
移项、合并同类项,得−x<2,
两边都除以−1,得x>−2.
解集在数轴上表示如答图③所示.

(4)去分母,得3(x+1)−2(x−1)<6,
去括号,得3x+3−2x+2<6,
移项、合并同类项,得x<1.
解集在数轴上表示如答图④所示.

2.解:(1)去分母,得2(2x+1)−6>3(1−x),
去括号,得4x+2−6>3−3x,
移项、合并同类项,得7x>7,
两边都除以7,得x>1.
解集在数轴上表示如答图①所示.

(2)去分母,得4x−(x+3)≥6,
去括号,得4x−x−3≥6,
移项、合并同类项,得3x≥9,
两边都除以3,得x≥3.
解集在数轴上表示如答图②所示,

(3)去分母,得2x+2−3x<4,
移项、合并同类项,得−x<2,
两边都除以−1,得x>−2.
解集在数轴上表示如答图③所示.

(4)去分母,得3(x+1)−2(x−1)<6,
去括号,得3x+3−2x+2<6,
移项、合并同类项,得x<1.
解集在数轴上表示如答图④所示.

3. 已知关于 $ x $ 的方程 $ 4 x + 2 m - 1 = 2 x + 5 $ 的解是负数.
(1) 求 $ m $ 的取值范围;
(2) 解关于 $ x $ 的不等式:$ x - 1 > \frac { m x + 1 } { 3 } $.
(1) 求 $ m $ 的取值范围;
(2) 解关于 $ x $ 的不等式:$ x - 1 > \frac { m x + 1 } { 3 } $.
答案:3.解:(1)方程4x+2m−1=2x+5的解是x=3−m.
由题意,得3−m<0,解得m>3.
(2)去分母,得3(x−1)>mx+1,
去括号,得3x−3>mx+1,
移项,得3x−mx>1+3,
合并同类项,得(3−m)x>4.
因为m>3,所以3−m<0,所以x<$\frac{4}{3−m}$.
由题意,得3−m<0,解得m>3.
(2)去分母,得3(x−1)>mx+1,
去括号,得3x−3>mx+1,
移项,得3x−mx>1+3,
合并同类项,得(3−m)x>4.
因为m>3,所以3−m<0,所以x<$\frac{4}{3−m}$.