7. 新情境 传统文化 《九章算术》中记载了“三畜食苗”的有趣问题:牛、马、羊吃了别人家的禾苗,禾苗主人要求赔偿,羊主人说:“我的羊吃了马一半的量。”马主人说:“我的马吃了牛一半的量。”若现在一共要赔偿 98 千克米,则牛主人应该赔偿(
56
)千克。答案:
7. 56 解析:根据题意,画图如下:

由图可知,羊主人应该赔偿 $98 ÷ (1 + 2 + 4) = 14$(千克),马主人应该赔偿 $14 × 2 = 28$(千克),牛主人应该赔偿 $28 × 2 = 56$(千克)。
7. 56 解析:根据题意,画图如下:

由图可知,羊主人应该赔偿 $98 ÷ (1 + 2 + 4) = 14$(千克),马主人应该赔偿 $14 × 2 = 28$(千克),牛主人应该赔偿 $28 × 2 = 56$(千克)。
8. 新情境 骑行比赛 骑行是一种健康又环保的生活方式,同时也能体现一种向上的生活态度。爸爸和妈妈进行骑行比赛,他们都在全长 250 米的椭圆形赛道上骑行了 3 圈。最终爸爸在领先妈妈 60 米时冲过终点,4 秒后妈妈到达终点。如果妈妈每秒多行 1 米,那么她能获胜吗?(比赛中两人的速度均不变)
答案:8. $250 × 3 = 750$(米) $60 ÷ 4 = 15$(米/秒) $750 ÷ 15 = 50$(秒) $50 - 4 = 46$(秒) $(15 + 1) × 46 = 736$(米) $736 < 750$ 她不能获胜。 解析:赛程是 $250 × 3 = 750$(米),妈妈的速度是 $60 ÷ 4 = 15$(米/秒),她骑完全程用了 $750 ÷ 15 = 50$(秒),则爸爸骑完全程用了 $50 - 4 = 46$(秒)。妈妈提速后的速度是 16 米/秒,此时她 46 秒可以骑行 $16 × 46 = 736$(米),而爸爸 46 秒可以骑行 750 米,$736 < 750$,所以她不能获胜。
解析:
$250×3=750$(米)
$60÷4=15$(米/秒)
$750÷15=50$(秒)
$50-4=46$(秒)
$(15+1)×46=736$(米)
$736<750$
她不能获胜。
$60÷4=15$(米/秒)
$750÷15=50$(秒)
$50-4=46$(秒)
$(15+1)×46=736$(米)
$736<750$
她不能获胜。
9. 新趋势 算理理解 玲玲和芳芳共折了 124 只纸鹤,玲玲比芳芳少折 28 只,玲玲和芳芳各折了多少只?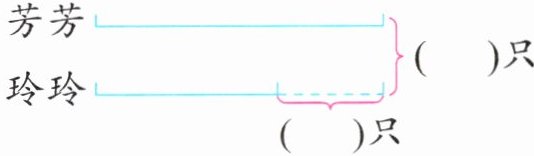
芳芳()只
玲玲()只
(1)把线段图补充完整。
(2)如果列式$(124 - 28)÷2$,求出的是(

芳芳()只
玲玲()只
(1)把线段图补充完整。
(2)如果列式$(124 - 28)÷2$,求出的是(
玲玲折了多少只纸鹤
);如果列式$(124 + 28)÷2$,求出的是(芳芳折了多少只纸鹤
)。答案:9. (1)28 124(从左往右) (2)玲玲折了多少只纸鹤 芳芳折了多少只纸鹤
10. 新趋势 算理理解 下面三位同学中,结合算式$4×3 + 7×3$,正确说明了乘法分配律成立的是(
华华:因为$4×3 + 7×3$一共是 10 个 3,所以$4×3 + 7×3 = (3 + 7)×3$。
同同:我用画图方法说明:
梦梦:我用举例方法说明:我到文具店买了单价 4 元/本的小练习本 3 本,单价 7 元/本的大练习本 3 本,求一共花了多少元。可以先分别求出大、小练习本各自花的钱数,再求一共花的钱数,也就是$4×3 + 7×3$;也可以先求大、小练习本的单价和,再求一共花的钱数,也就是$(4 + 7)×3$。
A.同同和华华
B.同同和梦梦
C.梦梦和华华
B
)。华华:因为$4×3 + 7×3$一共是 10 个 3,所以$4×3 + 7×3 = (3 + 7)×3$。
同同:我用画图方法说明:

梦梦:我用举例方法说明:我到文具店买了单价 4 元/本的小练习本 3 本,单价 7 元/本的大练习本 3 本,求一共花了多少元。可以先分别求出大、小练习本各自花的钱数,再求一共花的钱数,也就是$4×3 + 7×3$;也可以先求大、小练习本的单价和,再求一共花的钱数,也就是$(4 + 7)×3$。
A.同同和华华
B.同同和梦梦
C.梦梦和华华
答案:10. B
11. 新趋势 学科融合 在研究铜棒、铁棒、铝棒、塑料棒、木棒传热快慢的实验中,科学老师为了使实验效果更明显,数据更科学,课上他用电子温度计代替教材中提到的粘有凡士林的小珠子进行实验,数据记录如下。(单位:℃)
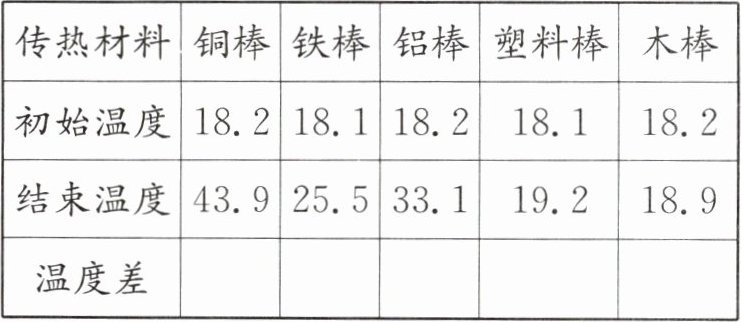
(1)完成表格。
(2)通过比较可知,(

(1)完成表格。
(2)通过比较可知,(
铜棒
)传热最快,(木棒
)传热最慢。答案:11. (1)25.7 7.4 14.9 1.1 0.7 (2)铜棒 木棒