跟踪练习2 亮点原创 马拉松长跑是国际上非常普及的长跑比赛项目,要求运动员在长时间内保持高强度的运动状态。甲、乙两人为备战一场马拉松长跑比赛,绕着一个长 400 米的环形跑道练习跑步。甲、乙两人从同一地点同时出发,背向而行,甲每分钟跑 280 米,乙每分钟跑 320 米。多少分钟后两人第三次相遇?
答案:400×3÷(280+320)=2(分)
解析 两人第三次相遇时合跑了3个全程。
解析 两人第三次相遇时合跑了3个全程。
例1 小芳每分钟行 90 米,小云每分钟行 80 米。两人从同一地点同时出发,相背而行,3 分钟后小芳转头去追小云,再经过多少分钟小芳能追上小云?
答案:
思路分析 这是行程问题中的追及问题,我们可以画出示意图来分析数量关系:
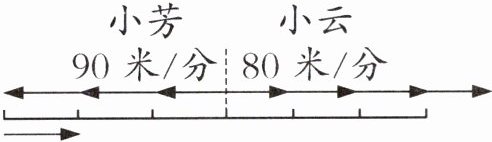
从图中可以看出,前 3 分钟两人之间的总路程就是小芳后来追赶小云的路程,先求出追赶的路程,即追及的路程,再用追及的路程除以速度差就可以求出小芳追上小云所用的时间。
规范解答 $(90 + 80)×3 = 510$(米)
$510÷(90 - 80) = 51$(分)
答:再经过 51 分钟小芳能追上小云。
技巧归纳
画出示意图,可以清晰地看到出发点和行走的方向,再根据对应的数量关系进行解答。解题时要学会辨别问题的类型,合理选用数量关系。
思路分析 这是行程问题中的追及问题,我们可以画出示意图来分析数量关系:

从图中可以看出,前 3 分钟两人之间的总路程就是小芳后来追赶小云的路程,先求出追赶的路程,即追及的路程,再用追及的路程除以速度差就可以求出小芳追上小云所用的时间。
规范解答 $(90 + 80)×3 = 510$(米)
$510÷(90 - 80) = 51$(分)
答:再经过 51 分钟小芳能追上小云。
技巧归纳
画出示意图,可以清晰地看到出发点和行走的方向,再根据对应的数量关系进行解答。解题时要学会辨别问题的类型,合理选用数量关系。
跟踪练习1 一辆货车和一辆客车从甲地开往乙地。货车出发 2 小时后客车才出发,结果客车开出 10 小时后与货车同时到达乙地。已知货车每小时行驶 80 千米,客车每小时行驶多少千米?
答案:80×2÷10=16(千米)
运算律
80+16=96(千米)
运算律
80+16=96(千米)
例2 甲、乙两人同时从两地骑自行车相向而行,甲每小时骑行 20 千米,乙每小时骑行 16 千米,两人相遇时距离中点 4 千米,全程长多少千米?
答案:
思路分析 根据题意画出线段图如下:
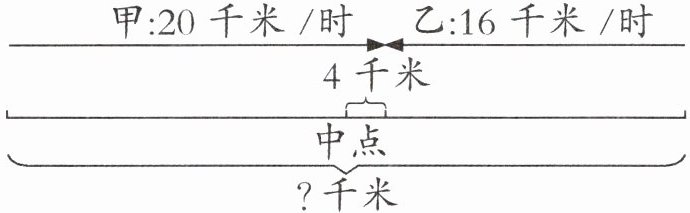
要求总路程,我们需要知道速度和与相遇时间。从图中可以分析出,相遇时甲比乙多骑行了$4×2 = 8$(千米),而甲每小时比乙多骑行$20 - 16 = 4$(千米),则相遇时间是$8÷4 = 2$(时),所以总路程为$(20 + 16)×2 = 72$(千米)。
规范解答 $4×2÷(20 - 16) = 2$(时)
$(20 + 16)×2 = 72$(千米)
答:全程长 72 千米。
技巧归纳
解决此类问题时有两点比较关键:一是根据离中点的距离确定两者的路程差是两个这样的距离;二是根据路程差和速度差求出相遇时间。
思路分析 根据题意画出线段图如下:

要求总路程,我们需要知道速度和与相遇时间。从图中可以分析出,相遇时甲比乙多骑行了$4×2 = 8$(千米),而甲每小时比乙多骑行$20 - 16 = 4$(千米),则相遇时间是$8÷4 = 2$(时),所以总路程为$(20 + 16)×2 = 72$(千米)。
规范解答 $4×2÷(20 - 16) = 2$(时)
$(20 + 16)×2 = 72$(千米)
答:全程长 72 千米。
技巧归纳
解决此类问题时有两点比较关键:一是根据离中点的距离确定两者的路程差是两个这样的距离;二是根据路程差和速度差求出相遇时间。