例1 下图中 $ ∠ 1 + ∠ 2 = 57° $,$ ∠ 3 = 14° $,$ ∠ 4 = 145° $,求 $ ∠ 2 $ 的度数。
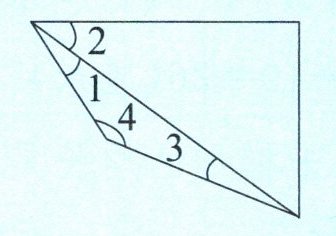

答案:思路分析 因为 $ ∠ 1 + ∠ 2 = 57° $,所以只要知道 $ ∠ 1 $ 的度数,就能求出 $ ∠ 2 $ 的度数。$ ∠ 1 $ 所在的三角形中其他两个内角的度数已知,利用三角形的内角和等于 $ 180° $ 可以求出 $ ∠ 1 $ 的度数。
规范解答 $ ∠ 1 = 180° - ∠ 3 - ∠ 4 = 180° - 14° - 145° = 21° $
$ ∠ 2 = 57° - ∠ 1 = 57° - 21° = 36° $
技巧归纳
明确三角形的内角和等于 $ 180° $ 是解决此题的关键。
规范解答 $ ∠ 1 = 180° - ∠ 3 - ∠ 4 = 180° - 14° - 145° = 21° $
$ ∠ 2 = 57° - ∠ 1 = 57° - 21° = 36° $
技巧归纳
明确三角形的内角和等于 $ 180° $ 是解决此题的关键。
跟踪练习1 (2025·无锡市期末)如图,已知 $ ∠ 1 = ∠ 5 = 90° $,$ ∠ 4 = 75° $,求 $ ∠ 3 $ 的度数。
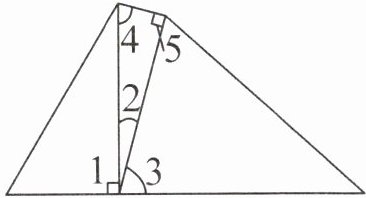

答案:∠2=180°−90°−75°=15°
∠3=180°−90°−15°=75°
解析 在中间的三角形中,∠2=180°−90°−75°=15°,又因为∠1+∠2+∠3=180°,所以∠3=180°−90°−15°=75°。
∠3=180°−90°−15°=75°
解析 在中间的三角形中,∠2=180°−90°−75°=15°,又因为∠1+∠2+∠3=180°,所以∠3=180°−90°−15°=75°。
跟踪练习2 如图是由梯形 $ ABCD $ 和等边三角形 $ CDE $ 组成的图形,求 $ ∠ 1 $ 的度数。
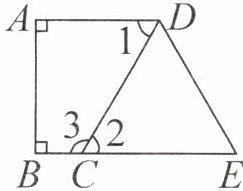

答案:∠3=180°−60°=120°
∠1=360°−90°−90°−120°=60°
∠1=360°−90°−90°−120°=60°
例2 一个等腰三角形的周长是 38 厘米,它的一条腰比底长 4 厘米。这个等腰三角形的底边长多少厘米?腰长多少厘米?
答案:
思路分析 根据题意画图分析如下:
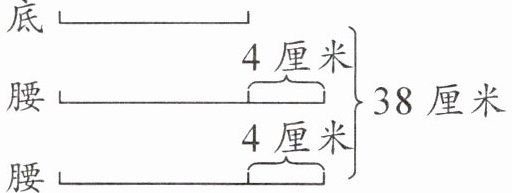
由图可知,从 38 厘米里去掉两个 4 厘米,就是底边长的 3 倍,由此可求出底边长 $ (38 - 4 - 4) ÷ 3 = 10 $(厘米),则腰长 $ 10 + 4 = 14 $(厘米)。
规范解答 $ (38 - 4 - 4) ÷ 3 = 10 $(厘米)
$ 10 + 4 = 14 $(厘米)
答:这个等腰三角形底边长 10 厘米,腰长 14 厘米。
技巧归纳
解决此类问题时,可以借助画线段图的方法将等腰三角形的两条腰、底和周长的关系直观地表示出来,并运用“多的减去”或“少的补上”的方法使“腰”和“底”变得同样长,进而解决问题。
思路分析 根据题意画图分析如下:

由图可知,从 38 厘米里去掉两个 4 厘米,就是底边长的 3 倍,由此可求出底边长 $ (38 - 4 - 4) ÷ 3 = 10 $(厘米),则腰长 $ 10 + 4 = 14 $(厘米)。
规范解答 $ (38 - 4 - 4) ÷ 3 = 10 $(厘米)
$ 10 + 4 = 14 $(厘米)
答:这个等腰三角形底边长 10 厘米,腰长 14 厘米。
技巧归纳
解决此类问题时,可以借助画线段图的方法将等腰三角形的两条腰、底和周长的关系直观地表示出来,并运用“多的减去”或“少的补上”的方法使“腰”和“底”变得同样长,进而解决问题。