例1
小力用竖式计算5.1加一个两位小数时,把加号看成了减号,得2.76。你能帮他算出正确的结果吗?
小力用竖式计算5.1加一个两位小数时,把加号看成了减号,得2.76。你能帮他算出正确的结果吗?
答案:思路分析:根据题意可知,5.1−()=2.76,利用“减数=被减数−差”可以求出这个两位小数,再用5.1加上这个两位小数就能得到正确的结果。
规范解答:
$5.1−2.76=2.34$
$5.1+2.34=7.44$
答:正确的结果是7.44。
技巧归纳:解题关键是根据看错运算符号的算式,求出另一个加数,再列出正确的算式进行计算。
规范解答:
$5.1−2.76=2.34$
$5.1+2.34=7.44$
答:正确的结果是7.44。
技巧归纳:解题关键是根据看错运算符号的算式,求出另一个加数,再列出正确的算式进行计算。
跟踪练习1(2025·淮安淮安区期末)小华用竖式计算6.2加一个两位小数时,把加号看成了减号,得4.56。这道题的正确结果应该是(
7.84
)。答案:[跟踪练习1] 7.84
解析:
6.2 - 4.56 = 1.64
6.2 + 1.64 = 7.84
6.2 + 1.64 = 7.84
例2
一个物体从高空下落,经过4秒落地。已知第一秒下落4.9米,以后每一秒都比前一秒多下落9.8米。这个物体在下落前距地面多少米?(先列表,再解答)
一个物体从高空下落,经过4秒落地。已知第一秒下落4.9米,以后每一秒都比前一秒多下落9.8米。这个物体在下落前距地面多少米?(先列表,再解答)
答案:
思路分析:首先需要理解“第一秒下落4.9米”和“以后每一秒都比前一秒多下落9.8米”的具体含义,即第二秒下落(4.9+9.8)米,第三秒下落(4.9+9.8+9.8)米,以此类推。
规范解答:
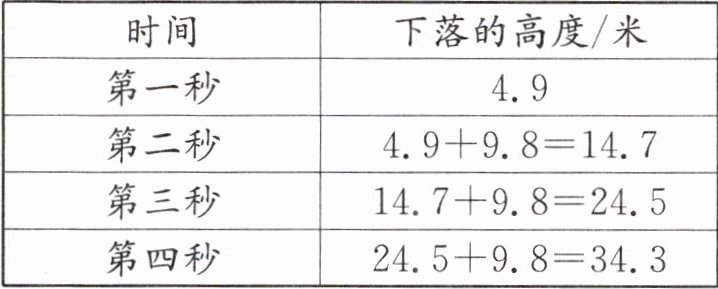
$4.9+14.7+24.5+34.3=78.4(米)$
答:这个物体在下落前距地面78.4米。
技巧归纳:解决比较复杂的小数加、减法的实际问题时,可以采用列表的方法帮助理解题意再解答。
思路分析:首先需要理解“第一秒下落4.9米”和“以后每一秒都比前一秒多下落9.8米”的具体含义,即第二秒下落(4.9+9.8)米,第三秒下落(4.9+9.8+9.8)米,以此类推。
规范解答:

$4.9+14.7+24.5+34.3=78.4(米)$
答:这个物体在下落前距地面78.4米。
技巧归纳:解决比较复杂的小数加、减法的实际问题时,可以采用列表的方法帮助理解题意再解答。
跟踪练习2小明骑自行车开始下坡,第一秒行驶0.7米,以后每秒都比前一秒多行驶1.2米,经过5秒后小明到达了坡底。这段下坡路有(
15.5
)米。答案:[跟踪练习2] 15.5 解析:根据题意列表整理出小明每秒行驶的路程。
第1秒 0.7米
第2秒 0.7+1.2=1.9(米)
第3秒 1.9+1.2=3.1(米)
第4秒 3.1+1.2=4.3(米)
第5秒 4.3+1.2=5.5(米)
由上表可知,小明5秒共行驶了0.7+1.9+3.1+4.3+5.5=15.5(米),即这段下坡路有15.5米。
第1秒 0.7米
第2秒 0.7+1.2=1.9(米)
第3秒 1.9+1.2=3.1(米)
第4秒 3.1+1.2=4.3(米)
第5秒 4.3+1.2=5.5(米)
由上表可知,小明5秒共行驶了0.7+1.9+3.1+4.3+5.5=15.5(米),即这段下坡路有15.5米。
例用简便方法计算下面各题。
(1)889+99.9+9.99+0.999+1.111
(2)6.43+8.36+8.57+2.64
(3)45.2−10.78−9.22
(1)889+99.9+9.99+0.999+1.111
(2)6.43+8.36+8.57+2.64
(3)45.2−10.78−9.22
答案:思路分析:观察数据的特点可知,第(1)题可凑整计算,第(2)(3)题可用加法运算律和减法的性质简便计算。
规范解答:
(1)
$\begin{aligned}&889+99.9+9.99+0.999+1.111\\=&889+99.9+9.99+0.999+(1+0.1+0.01+0.001)\\=&(889+1)+(99.9+0.1)+(9.99+0.01)+(0.999+0.001)\\=&890+100+10+1\\=&1001\end{aligned}$
(2)
$\begin{aligned}&6.43+8.36+8.57+2.64\\=&(6.43+8.57)+(8.36+2.64)\\=&15+11\\=&26\end{aligned}$
(3)
$\begin{aligned}&45.2−10.78−9.22\\=&45.2−(10.78+9.22)\\=&45.2−20\\=&25.2\end{aligned}$
技巧归纳:整数加、减法的运算律和运算性质同样适用于小数加、减法的运算。
规范解答:
(1)
$\begin{aligned}&889+99.9+9.99+0.999+1.111\\=&889+99.9+9.99+0.999+(1+0.1+0.01+0.001)\\=&(889+1)+(99.9+0.1)+(9.99+0.01)+(0.999+0.001)\\=&890+100+10+1\\=&1001\end{aligned}$
(2)
$\begin{aligned}&6.43+8.36+8.57+2.64\\=&(6.43+8.57)+(8.36+2.64)\\=&15+11\\=&26\end{aligned}$
(3)
$\begin{aligned}&45.2−10.78−9.22\\=&45.2−(10.78+9.22)\\=&45.2−20\\=&25.2\end{aligned}$
技巧归纳:整数加、减法的运算律和运算性质同样适用于小数加、减法的运算。