1. 杆秤是我国传统的计重工具. 它制作轻巧、经典, 使用也极为便利, 作为商品流通的度量工具,活跃在大江南北, 代代相传. 天地间有杆秤, 人们不断赋予秤新的文化内涵, 公平公正的象征,天地良心的标尺, 一桩桩交易就在秤砣与秤盘的此起彼伏间完成.
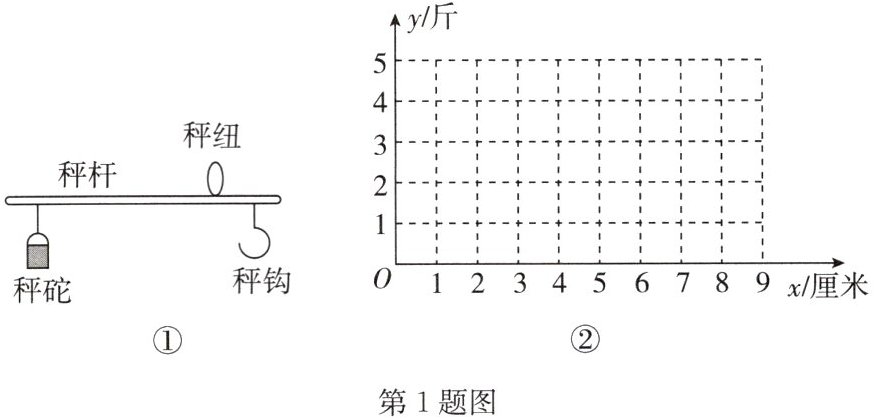
【建立模型】如图①, 可以用秤砣到秤纽的水平距离得出秤钩上所挂物体的质量. 称重时, 若秤杆上秤砣到秤纽的水平距离为 $ x $ (厘米) 时, 秤钩所挂物重为 $ y $ (斤), 则 $ y $ 是 $ x $ 的一次函数, 下表为校准秤杆时若干次称重所记录的一些数据.
| $ x $/厘米 | 1 | 2 | 3 | 4 | 5 | 6 |
| --- | --- | --- | --- | --- | --- | --- |
| $ y $/斤 | 0.6 | 1.3 | 2 | 2.7 | 3.4 | 4.8 |
【解决问题】
(1) 在上表 $ x, y $ 的数据中, 发现有一对数据记录错误, 在图②中, 通过描点的方法, 观察并判断哪一对数是错误的, 以坐标的形式表示出来.
(2) 秤杆上秤砣到秤纽的水平距离 $ x $ 每增加 1 厘米时, 秤钩所挂物重 $ y $ 增加______斤.
(3) 根据表格和图, 通过计算回答下列问题.
① 求 $ y $ 与 $ x $ 之间的函数表达式;
② 当秤钩所挂物重是 6.2 斤时, 问秤杆上秤砣到秤纽的水平距离为多少厘米?
【建立模型】如图①, 可以用秤砣到秤纽的水平距离得出秤钩上所挂物体的质量. 称重时, 若秤杆上秤砣到秤纽的水平距离为 $ x $ (厘米) 时, 秤钩所挂物重为 $ y $ (斤), 则 $ y $ 是 $ x $ 的一次函数, 下表为校准秤杆时若干次称重所记录的一些数据.
| $ x $/厘米 | 1 | 2 | 3 | 4 | 5 | 6 |
| --- | --- | --- | --- | --- | --- | --- |
| $ y $/斤 | 0.6 | 1.3 | 2 | 2.7 | 3.4 | 4.8 |
【解决问题】
(1) 在上表 $ x, y $ 的数据中, 发现有一对数据记录错误, 在图②中, 通过描点的方法, 观察并判断哪一对数是错误的, 以坐标的形式表示出来.
(2) 秤杆上秤砣到秤纽的水平距离 $ x $ 每增加 1 厘米时, 秤钩所挂物重 $ y $ 增加______斤.
(3) 根据表格和图, 通过计算回答下列问题.
① 求 $ y $ 与 $ x $ 之间的函数表达式;
② 当秤钩所挂物重是 6.2 斤时, 问秤杆上秤砣到秤纽的水平距离为多少厘米?

答案:
(1)解:把表中数据描点如答图.

观察图象可知:由于y是x的一次函数,$(6,4.8)$没有位于直线上,
$\therefore x=6,y=4.8$这组数据错误,
故$(6,4.8)$是错误的.
(2)0.7
(3)解:①$\because y$是$x$的一次函数,$\therefore$设$y$与$x$的函数表达式为$y=kx+b$,将$(1,0.6),(2,1.3)$代入得$\left\{\begin{array}{l} k+b=0.6,\\ 2k+b=1.3,\end{array}\right. $
解得$\left\{\begin{array}{l} k=0.7,\\ b=-0.1,\end{array}\right. $
$\therefore y$与$x$之间的函数表达式为$y=0.7x-0.1$.
②当$y=6.2$时,$6.2=0.7x-0.1$,解得$x=9$.
答:当秤钩所挂物重是6.2斤时,秤杆上秤砣到秤纽的水平距离为9厘米.
(1)解:把表中数据描点如答图.

观察图象可知:由于y是x的一次函数,$(6,4.8)$没有位于直线上,
$\therefore x=6,y=4.8$这组数据错误,
故$(6,4.8)$是错误的.
(2)0.7
(3)解:①$\because y$是$x$的一次函数,$\therefore$设$y$与$x$的函数表达式为$y=kx+b$,将$(1,0.6),(2,1.3)$代入得$\left\{\begin{array}{l} k+b=0.6,\\ 2k+b=1.3,\end{array}\right. $
解得$\left\{\begin{array}{l} k=0.7,\\ b=-0.1,\end{array}\right. $
$\therefore y$与$x$之间的函数表达式为$y=0.7x-0.1$.
②当$y=6.2$时,$6.2=0.7x-0.1$,解得$x=9$.
答:当秤钩所挂物重是6.2斤时,秤杆上秤砣到秤纽的水平距离为9厘米.