2. 问题情境: 在物理学中有很多公式可以直接或者间接看成一次函数, 例如, 在弹性限度内, 弹簧的长度随着拉力的增大而不断地增加, 当弹簧所受的外力过大时, 会损坏它的弹性, 使得弹簧被拉到最长且无法复原. 某班在实践课上对“弹簧的长度与所受外力之间的关系”进行了探究.
方案设计: “智慧小组”在探究弹簧测力器的“弹簧的长度与所受外力之间的关系”时, 多次改变砝码的质量 $ x $ (单位: $ g $), 测量得到弹簧的长度 $ y $ (单位: $ cm $), 且通过实验记录得到的数据如表所示:
| 砝码的质量 $ x/g $ | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 弹簧的长度 $ y/cm $ | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
如图, “智慧小组”根据实验数据, 建立平面直角坐标系, 并绘制了部分图.
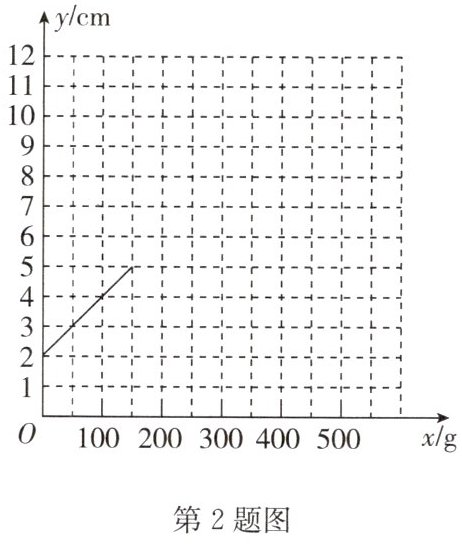
问题解决:
(1) 表格中的数据反映了两个变量之间的关系, 其中自变量是______.
(2) 在弹性限度内, 求弹簧的长度 $ y $ 与所挂砝码的质量 $ x $ 之间的函数表达式; 当砝码的质量为 $ 75g $ 时, 求弹簧的长度.
(3) 根据表格数据, 在平面直角坐标系中描点并连线, 补全该函数的图象.
(4) 根据图象, 在不损坏该弹簧的情况下, 所挂砝码的质量应不超过______ $ g $.
方案设计: “智慧小组”在探究弹簧测力器的“弹簧的长度与所受外力之间的关系”时, 多次改变砝码的质量 $ x $ (单位: $ g $), 测量得到弹簧的长度 $ y $ (单位: $ cm $), 且通过实验记录得到的数据如表所示:
| 砝码的质量 $ x/g $ | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 弹簧的长度 $ y/cm $ | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
如图, “智慧小组”根据实验数据, 建立平面直角坐标系, 并绘制了部分图.

问题解决:
(1) 表格中的数据反映了两个变量之间的关系, 其中自变量是______.
(2) 在弹性限度内, 求弹簧的长度 $ y $ 与所挂砝码的质量 $ x $ 之间的函数表达式; 当砝码的质量为 $ 75g $ 时, 求弹簧的长度.
(3) 根据表格数据, 在平面直角坐标系中描点并连线, 补全该函数的图象.
(4) 根据图象, 在不损坏该弹簧的情况下, 所挂砝码的质量应不超过______ $ g $.
答案:
(1)砝码的质量$x$
(2)解:设$y=kx+b$,
将$(0,2),(50,3)$代入得$\left\{\begin{array}{l} b=2,\\ 50k+b=3,\end{array}\right. $解得$\left\{\begin{array}{l} k=\frac {1}{50},\\ b=2,\end{array}\right. $
$\therefore y=\frac {1}{50}x+2$.
当$x=75$时,$y=\frac {75}{50}+2=3.5$,
$\therefore$当砝码的质量为75g时,弹簧的长度为3.5cm.
(3)解:如答图.
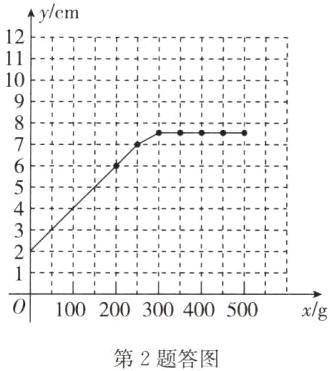
(4)250
(1)砝码的质量$x$
(2)解:设$y=kx+b$,
将$(0,2),(50,3)$代入得$\left\{\begin{array}{l} b=2,\\ 50k+b=3,\end{array}\right. $解得$\left\{\begin{array}{l} k=\frac {1}{50},\\ b=2,\end{array}\right. $
$\therefore y=\frac {1}{50}x+2$.
当$x=75$时,$y=\frac {75}{50}+2=3.5$,
$\therefore$当砝码的质量为75g时,弹簧的长度为3.5cm.
(3)解:如答图.

(4)250