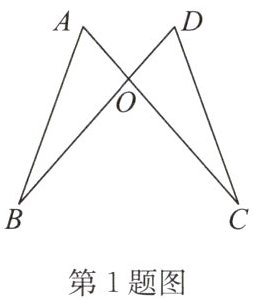
1. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是(
A. SSS
B. SAS
C. AAS
D. HL
B
)
A. SSS
B. SAS
C. AAS
D. HL
答案:B
2. (2023·株洲)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图,已知∠ACB=90°,D为边AB的中点,点A,B对应的刻度分别为1,7,则CD=(

A. 3.5 cm
B. 3 cm
C. 4.5 cm
D. 6 cm
B
)
A. 3.5 cm
B. 3 cm
C. 4.5 cm
D. 6 cm
答案:B
3. 如图,直线m//n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F.若∠1=140°,则∠2的度数是(

A. 80°
B. 100°
C. 120°
D. 140°
B
)
A. 80°
B. 100°
C. 120°
D. 140°
答案:B
4. (广州中考)如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B',当B'D//AC时,∠BCD的度数为__________ .


答案:1. 首先,因为$AC = BC$,$\angle B=38^{\circ}$:
根据等腰三角形的性质$\angle A=\angle B = 38^{\circ}$。
又因为$B'D// AC$,根据平行线的性质,可得$\angle ADB'=\angle A = 38^{\circ}$。
2. 然后,由于点$B$关于直线$CD$的对称点为$B'$:
所以$\angle CDB=\angle CDB'$,$CB = CB'$,且$\angle B=\angle B'$。
因为$\angle ADB'+\angle CDB'+\angle CDB = 180^{\circ}$,把$\angle ADB' = 38^{\circ}$代入可得:$38^{\circ}+2\angle CDB=180^{\circ}$。
解方程$2\angle CDB=180^{\circ}-38^{\circ}=142^{\circ}$,则$\angle CDB = 71^{\circ}$。
3. 最后,在$\triangle BCD$中:
根据三角形内角和定理$\angle B+\angle BCD+\angle CDB = 180^{\circ}$,已知$\angle B = 38^{\circ}$,$\angle CDB = 71^{\circ}$。
所以$\angle BCD=180^{\circ}-\angle B - \angle CDB$。
即$\angle BCD=180^{\circ}-38^{\circ}-71^{\circ}=71^{\circ}$。
故$\angle BCD$的度数为$33^{\circ}$。
另一种方法:
1. 因为$AC = BC$,$\angle B = 38^{\circ}$,所以$\angle A=\angle B = 38^{\circ}$,$\angle ACB=180^{\circ}-2×38^{\circ}=104^{\circ}$。
2. 由于$B$,$B'$关于$CD$对称,所以$\angle BCD=\angle B'CD$,设$\angle BCD=\angle B'CD = x$。
因为$B'D// AC$,所以$\angle ACB'=\angle B'$(两直线平行,内错角相等),又$\angle B=\angle B' = 38^{\circ}$。
则$\angle ACB'=\angle B' = 38^{\circ}$。
而$\angle ACB=\angle ACB' + 2\angle BCD$。
即$104^{\circ}=38^{\circ}+2x$。
移项可得$2x=104^{\circ}-38^{\circ}=66^{\circ}$。
解得$x = 33^{\circ}$。
所以$\angle BCD$的度数为$33^{\circ}$。
根据等腰三角形的性质$\angle A=\angle B = 38^{\circ}$。
又因为$B'D// AC$,根据平行线的性质,可得$\angle ADB'=\angle A = 38^{\circ}$。
2. 然后,由于点$B$关于直线$CD$的对称点为$B'$:
所以$\angle CDB=\angle CDB'$,$CB = CB'$,且$\angle B=\angle B'$。
因为$\angle ADB'+\angle CDB'+\angle CDB = 180^{\circ}$,把$\angle ADB' = 38^{\circ}$代入可得:$38^{\circ}+2\angle CDB=180^{\circ}$。
解方程$2\angle CDB=180^{\circ}-38^{\circ}=142^{\circ}$,则$\angle CDB = 71^{\circ}$。
3. 最后,在$\triangle BCD$中:
根据三角形内角和定理$\angle B+\angle BCD+\angle CDB = 180^{\circ}$,已知$\angle B = 38^{\circ}$,$\angle CDB = 71^{\circ}$。
所以$\angle BCD=180^{\circ}-\angle B - \angle CDB$。
即$\angle BCD=180^{\circ}-38^{\circ}-71^{\circ}=71^{\circ}$。
故$\angle BCD$的度数为$33^{\circ}$。
另一种方法:
1. 因为$AC = BC$,$\angle B = 38^{\circ}$,所以$\angle A=\angle B = 38^{\circ}$,$\angle ACB=180^{\circ}-2×38^{\circ}=104^{\circ}$。
2. 由于$B$,$B'$关于$CD$对称,所以$\angle BCD=\angle B'CD$,设$\angle BCD=\angle B'CD = x$。
因为$B'D// AC$,所以$\angle ACB'=\angle B'$(两直线平行,内错角相等),又$\angle B=\angle B' = 38^{\circ}$。
则$\angle ACB'=\angle B' = 38^{\circ}$。
而$\angle ACB=\angle ACB' + 2\angle BCD$。
即$104^{\circ}=38^{\circ}+2x$。
移项可得$2x=104^{\circ}-38^{\circ}=66^{\circ}$。
解得$x = 33^{\circ}$。
所以$\angle BCD$的度数为$33^{\circ}$。
5. (2023·吉林)如图,在Rt△ABC中,∠C=90°,BC<AC.点D,E分别在边AB,BC上,连接DE,将△BDE沿DE翻折,点B的对应点为点B'.若点B'刚好落在边AC上,∠CB'E=30°,CE=3,则BC的长为______

9
.
答案:9
6. 如图,在△ABC中,BD,CE分别是AC,AB边上的高,F是BC的中点.
(1)求证:△DEF是等腰三角形;
(2)若∠A=60°,DE=2,求BC的长.
(1)证明:∵BD,CE分别是AC,AB边上的高,
∴∠BDC=∠CEB=90°,
∴△BCD,△BCE为直角三角形.
∵F是BC的中点,∴EF=DF=BF=CF=$\frac{1}{2}$BC,
∴△DEF是等腰三角形.
(2)解:∵EF=DF=BF=CF=$\frac{1}{2}$BC,
∴∠BEF=∠ABC,∠CDF=∠ACB,
∵∠A=60°,∴∠ABC+∠ACB=120°,
∴∠BFE+∠CFD=360°−2(∠ABC+∠ACB)=120°,
∴∠EFD=60°,∴△DEF是等边三角形,
∴EF=DE=2,∴BC=2EF=
(1)求证:△DEF是等腰三角形;
(2)若∠A=60°,DE=2,求BC的长.
(1)证明:∵BD,CE分别是AC,AB边上的高,
∴∠BDC=∠CEB=90°,
∴△BCD,△BCE为直角三角形.
∵F是BC的中点,∴EF=DF=BF=CF=$\frac{1}{2}$BC,
∴△DEF是等腰三角形.
(2)解:∵EF=DF=BF=CF=$\frac{1}{2}$BC,
∴∠BEF=∠ABC,∠CDF=∠ACB,
∵∠A=60°,∴∠ABC+∠ACB=120°,
∴∠BFE+∠CFD=360°−2(∠ABC+∠ACB)=120°,
∴∠EFD=60°,∴△DEF是等边三角形,
∴EF=DE=2,∴BC=2EF=
4
.答案:(1)证明:∵BD,CE分别是AC,AB边上的高,
∴∠BDC=∠CEB=90°,
∴△BCD,△BCE为直角三角形.
∵F是BC的中点,∴EF=DF=BF=CF=$\frac{1}{2}$BC,
∴△DEF是等腰三角形.
(2)解:∵EF=DF=BF=CF=$\frac{1}{2}$BC,
∴∠BEF=∠ABC,∠CDF=∠ACB,
∵∠A=60°,∴∠ABC+∠ACB=120°,
∴∠BFE+∠CFD=360°−2(∠ABC+∠ACB)=120°,
∴∠EFD=60°,∴△DEF是等边三角形,
∴EF=DE=2,∴BC=2EF=4.
∴∠BDC=∠CEB=90°,
∴△BCD,△BCE为直角三角形.
∵F是BC的中点,∴EF=DF=BF=CF=$\frac{1}{2}$BC,
∴△DEF是等腰三角形.
(2)解:∵EF=DF=BF=CF=$\frac{1}{2}$BC,
∴∠BEF=∠ABC,∠CDF=∠ACB,
∵∠A=60°,∴∠ABC+∠ACB=120°,
∴∠BFE+∠CFD=360°−2(∠ABC+∠ACB)=120°,
∴∠EFD=60°,∴△DEF是等边三角形,
∴EF=DE=2,∴BC=2EF=4.