11. 任何实数$a$,可用$[a]$表示不超过$a$的最大整数,如$[4]=4,[\sqrt{3}]=1$. 现对 72 进行如下操作:$72\xrightarrow{第一次}[\sqrt{72}]=8\xrightarrow{第二次}[\sqrt{8}]=2\xrightarrow{第三次}[\sqrt{2}]=1$,这样对 72 进行 3 次操作后变为 1,类似地,对 81 进行 3 次操作后变为 1. 那么只需进行 3 次操作就可变为 1 的所有正整数中,最大的是______
255
.答案:255
12. 如图,实数$-\sqrt{5},\sqrt{15},m$在数轴上所对应的点分别为$A,B,C$,点$B$关于原点$O$的对称点为$D$. 若$m$为整数,则$m$的值为______
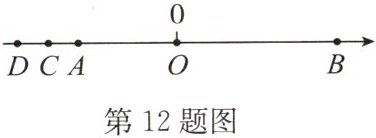
-3
.
答案:- 3
13. (2023 春·海安月考)对于实数$a$,我们规定用$\{\sqrt{a}\}$表示不小于$\sqrt{a}$的最小整数,称$\{\sqrt{a}\}$为$a$的根整数. 如$\{\sqrt{10}\}=4$.
(1)计算$\{\sqrt{9}\}=$
(2)现对$a$进行连续求根整数,直到结果为 2 为止,例如,对 12 进行连续求根整数,第一次$\{\sqrt{12}\}=4$,再进行第二次求根整数$\{\sqrt{4}\}=2$,表示对 12 连续求根整数 2 次可得结果为 2. 对 101 进行连续求根整数,
(3)若$\{\sqrt{m}\}=3$,写出满足题意的$m$的整数值.
(1)计算$\{\sqrt{9}\}=$
3
;(2)现对$a$进行连续求根整数,直到结果为 2 为止,例如,对 12 进行连续求根整数,第一次$\{\sqrt{12}\}=4$,再进行第二次求根整数$\{\sqrt{4}\}=2$,表示对 12 连续求根整数 2 次可得结果为 2. 对 101 进行连续求根整数,
3
次后结果为 2;(3)若$\{\sqrt{m}\}=3$,写出满足题意的$m$的整数值.
答案:(1)3 (2)3
(3)解:∵{$\sqrt{m}$}=3,∴2<$\sqrt{m}$≤3,∴4<m≤9,
∴满足题意的m的整数值为5,6,7,8,9.
(3)解:∵{$\sqrt{m}$}=3,∴2<$\sqrt{m}$≤3,∴4<m≤9,
∴满足题意的m的整数值为5,6,7,8,9.
14. 如图,点$A$是数轴上表示实数$a$的点.
(1)用直尺和圆规在数轴上作出表示实数$\sqrt{2}$的点$P$;(保留作图痕迹,不写作法)
(2)利用数轴比较$\sqrt{2}$和$a$的大小,并说明理由.

(1)用直尺和圆规在数轴上作出表示实数$\sqrt{2}$的点$P$;(保留作图痕迹,不写作法)
(2)利用数轴比较$\sqrt{2}$和$a$的大小,并说明理由.

答案:
解:(1)如答图,点P即为所求.
(2)a>$\sqrt{2}$,理由如下:
如答图,点A在点P的右侧,∴a>$\sqrt{2}$.

解:(1)如答图,点P即为所求.
(2)a>$\sqrt{2}$,理由如下:
如答图,点A在点P的右侧,∴a>$\sqrt{2}$.

15. 为了比较$\sqrt{5}+1$与$\sqrt{10}$的大小,小伍和小陆两名同学对这个问题分别进行了研究.
(1)小伍同学利用计算器得到了$\sqrt{5}\approx 2.236,\sqrt{10}\approx 3.162$,所以确定$\sqrt{5}+1$
(2)小陆同学受到前面学习在数轴上用点表示无理数的启发,构造出如图所示的图形,其中$∠C = 90^{\circ},BC = 3$,点$D$在$BC$上,且$BD = AC = 1$. 请你利用此图进行计算与推理,帮小陆同学判断$\sqrt{5}+1$和$\sqrt{10}$的大小.

(1)小伍同学利用计算器得到了$\sqrt{5}\approx 2.236,\sqrt{10}\approx 3.162$,所以确定$\sqrt{5}+1$
>
$\sqrt{10}$;(填“>”“<”或“=”)(2)小陆同学受到前面学习在数轴上用点表示无理数的启发,构造出如图所示的图形,其中$∠C = 90^{\circ},BC = 3$,点$D$在$BC$上,且$BD = AC = 1$. 请你利用此图进行计算与推理,帮小陆同学判断$\sqrt{5}+1$和$\sqrt{10}$的大小.

答案:(1)>
(2)解:∵∠C=90°,BC=3,BD=AC=1,∴CD=2,
∴AD=$\sqrt{CD²+AC²}$=$\sqrt{5}$,AB=$\sqrt{AC²+BC²}$=$\sqrt{10}$,∴BD+AD=$\sqrt{5}$+1.
又∵△ABD中,AD+BD>AB,∴$\sqrt{5}$+1>$\sqrt{10}$
(2)解:∵∠C=90°,BC=3,BD=AC=1,∴CD=2,
∴AD=$\sqrt{CD²+AC²}$=$\sqrt{5}$,AB=$\sqrt{AC²+BC²}$=$\sqrt{10}$,∴BD+AD=$\sqrt{5}$+1.
又∵△ABD中,AD+BD>AB,∴$\sqrt{5}$+1>$\sqrt{10}$