1.《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数a,b,c的计算公式:$a=\frac {1}{2}(m^{2}-n^{2}),b=mn,c=\frac {1}{2}(m^{2}+n^{2})$,其中$m＞n＞0$,m,n是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是 ()
A. 3,4,5
B. 5,12,13
C. 6,8,10
D. 7,24,25

2.如图,直角三角形三边上的等边三角形的面积从小到大依次记为$S_{1},S_{2},S_{3}$,则$S_{1},S_{2},S_{3}$之间的关系是 ()

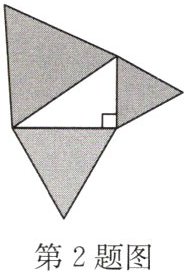
A.$S_{1}+S_{2}＞S_{3}$
B.$S_{1}+S_{2}＜S_{3}$
C.$S_{1}+S_{2}=S_{3}$
D.$S_{1}^{2}+S_{2}^{2}＞S_{3}^{2}$

3.如图,在$Rt△ABC$中,$∠C=90^{\circ },∠BAC$的平分线交 BC 于点 D,$DE// AB$,交 AC 于点 E,$DF⊥AB$于点F,$DE=5,DF=3$,则下列结论错误的是 ()

A.$BF=1$
B.$DC=3$
C.$AE=5$
D.$AC=9$

4.(2023·随州)如图,在$Rt△ABC$中,$∠C=90^{\circ },AC=8,BC=6$,D为AC上一点,若BD是$∠ABC$的平分线,则$AD=$.

5.(绥化中考)在$Rt△ABC$中,$∠C=90^{\circ }$,若$AB-AC=2,BC=8$,则 AB 的长是____.

6.(2023·仪征期末)如图,在$Rt△ABC$中,$∠B=90^{\circ },AB=3,BC=4,$$AD=12,CD=13$,点 E 是 CD 的中点,求 AE 的长.

解:在Rt△ABC中,∠B = 90°,∵AB = 3,BC = 4,
　∴AC = $\sqrt{AB^{2} + BC^{2}}$ = $\sqrt{3^{2} + 4^{2}}$ = ,
　∵AD = 12,CD = 13,
　AC² + AD² = 5² + 12² = 169,CD² = 169,
　∴AC² + AD² = CD²,∴∠DAC = ,
　∴△ACD是直角三角形.
　∵点E是CD的中点,∴AE = $\frac{1}{2}$CD = $\frac{1}{2}$×13 = .

7.(2023·泰州模拟)以直角三角形的各边为边分别向外作正方形(如图①),再把较小的两个正方形按图②的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ()

A.四边形 ABCD 的面积
B.四边形 DCEG 的面积
C.四边形 HGFP 的面积
D.$△GEF$的面积