8.如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为
$\sqrt{2}$
.答案:$\sqrt{2}$
9.在$△ABC$中,$AB=15,AC=13$,高$AD=12$,则$△ABC$的周长为
42或32
.答案:42或32
10.现用4个全等的直角三角形拼成如图所示的“弦图”.在$Rt△ABC$中,$∠ACB=90^{\circ }$,若$AC=b,BC=a,AB=c$.请你利用这个图形解决下列问题:
(1)试说明$a^{2}+b^{2}=c^{2}$;
(2)如果大正方形的面积是6,小正方形的面积是2,求$(a+b)^{2}$的值.
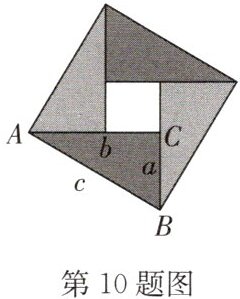
(1)∵大正方形的面积为$c²$,直角三角形的面积为$\frac{1}{2}$ab,小正方形的面积为$(b - a)²$,
∴$c² = 4×\frac{1}{2}ab + (a - b)² = 2ab + a² - 2ab + b²$,
即$c² = a² + b²$.
(2)由题意可知,$(b - a)²=2$,$4×\frac{1}{2}ab=6 - 2=4$,
∴$ab=2$,∴$(a + b)²=(b - a)² + 4ab=$
(1)试说明$a^{2}+b^{2}=c^{2}$;
(2)如果大正方形的面积是6,小正方形的面积是2,求$(a+b)^{2}$的值.

(1)∵大正方形的面积为$c²$,直角三角形的面积为$\frac{1}{2}$ab,小正方形的面积为$(b - a)²$,
∴$c² = 4×\frac{1}{2}ab + (a - b)² = 2ab + a² - 2ab + b²$,
即$c² = a² + b²$.
(2)由题意可知,$(b - a)²=2$,$4×\frac{1}{2}ab=6 - 2=4$,
∴$ab=2$,∴$(a + b)²=(b - a)² + 4ab=$
10
.答案:解:(1)∵大正方形的面积为c²,直角三角形的面积为$\frac{1}{2}$ab,小正方形的面积为(b - a)²,
∴c² = 4×$\frac{1}{2}$ab + (a - b)² = 2ab + a² - 2ab + b²,
即c² = a² + b².
(2)由题意可知,(b - a)² = 2,4×$\frac{1}{2}$ab = 6 - 2 = 4,
∴ab = 2,∴(a + b)² = (b - a)² + 4ab = 10.
∴c² = 4×$\frac{1}{2}$ab + (a - b)² = 2ab + a² - 2ab + b²,
即c² = a² + b².
(2)由题意可知,(b - a)² = 2,4×$\frac{1}{2}$ab = 6 - 2 = 4,
∴ab = 2,∴(a + b)² = (b - a)² + 4ab = 10.
11.如图,在$△ABC$中,$AC=21,BC=13$,D 是 AC 边上一点,$BD=12,AD=16$.
(1)若 E 是边 AB 的中点,求线段 DE 的长;
(2)若 E 是边 AB 上的动点,求线段 DE 长度的最小值.

(1)若 E 是边 AB 的中点,求线段 DE 的长;
10
(2)若 E 是边 AB 上的动点,求线段 DE 长度的最小值.
$\frac{48}{5}$

答案:解:(1)在△BCD中,BC = 13,BD = 12,CD = AC - AD = 5,
∵5² + 12² = 169 = 13²,即CD² + BD² = BC²,
∴∠BDC = 90°.
在Rt△ABD中,AD = 16,BD = 12,∠ADB = 90°,
∴AB = $\sqrt{AD^{2} + BD^{2}}$ = 20.
又∵点E是边AB的中点,∴DE = $\frac{1}{2}$AB = 10.
(2)当DE⊥AB时,DE长度最小.
此时S△ABD = $\frac{1}{2}$AD·BD = $\frac{1}{2}$AB·DE,
∴DE = $\frac{AD·BD}{AB}$ = $\frac{48}{5}$.
∴线段DE长度的最小值为$\frac{48}{5}$.
∵5² + 12² = 169 = 13²,即CD² + BD² = BC²,
∴∠BDC = 90°.
在Rt△ABD中,AD = 16,BD = 12,∠ADB = 90°,
∴AB = $\sqrt{AD^{2} + BD^{2}}$ = 20.
又∵点E是边AB的中点,∴DE = $\frac{1}{2}$AB = 10.
(2)当DE⊥AB时,DE长度最小.
此时S△ABD = $\frac{1}{2}$AD·BD = $\frac{1}{2}$AB·DE,
∴DE = $\frac{AD·BD}{AB}$ = $\frac{48}{5}$.
∴线段DE长度的最小值为$\frac{48}{5}$.
12.如图,$△ABC$中,$∠ACB=90^{\circ },AB=10cm,BC=6cm$,若点 P 从点 A 出发,以每秒 1 cm 的速度沿折线$A-C-B-A$运动,设运动时间为$ts(t>0)$.
(1)当点 P 在 AC 上,且满足$PA=PB$时,求出此时 t 的值;
(2)当点 P 在 AB 上时,求出 t 为何值时,$△BCP$为等腰三角形.

(1)当点 P 在 AC 上,且满足$PA=PB$时,求出此时 t 的值;
(2)当点 P 在 AB 上时,求出 t 为何值时,$△BCP$为等腰三角形.

答案:
解:(1)∵△ABC中,∠ACB = 90°,AB = 10,BC = 6,
∴由勾股定理得AC = $\sqrt{10^{2} - 6^{2}}$ = 8,
当PA = PB时,PA = PB = t,PC = 8 - t,
在Rt△PCB中,PC² + CB² = PB²,
即(8 - t)² + 6² = t²,解得t = $\frac{25}{4}$,
∴当t = $\frac{25}{4}$时,PA = PB.
(2)如答图①,当BP = BC = 6时,△BCP为等腰三角形,
∴AC + CB + BP = 8 + 6 + 6 = 20,
∴t = 20÷1 = 20;
如答图②,当CP = CB = 6时,作CD⊥AB于点D,则根据面积法求得CD = 4.8,
在Rt△BCD中,由勾股定理得,BD = 3.6,
∴PB = 2BD = 7.2,
∴CA + CB + BP = 8 + 6 + 7.2 = 21.2,
此时t = 21.2÷1 = 21.2;
如答图③,当PC = PB时,作PD⊥BC于点D,作PE⊥AC于点E,则D为BC的中点,可证△APE≌△PBD.
∴AP = BP = $\frac{1}{2}$AB = 5,
∴AC + CB + BP = 8 + 6 + 5 = 19,∴t = 19÷1 = 19.
综上所述,t为20或21.2或19时,△BCP为等腰三角形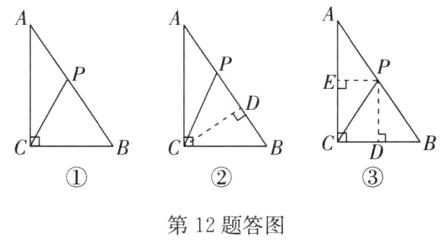
解:(1)∵△ABC中,∠ACB = 90°,AB = 10,BC = 6,
∴由勾股定理得AC = $\sqrt{10^{2} - 6^{2}}$ = 8,
当PA = PB时,PA = PB = t,PC = 8 - t,
在Rt△PCB中,PC² + CB² = PB²,
即(8 - t)² + 6² = t²,解得t = $\frac{25}{4}$,
∴当t = $\frac{25}{4}$时,PA = PB.
(2)如答图①,当BP = BC = 6时,△BCP为等腰三角形,
∴AC + CB + BP = 8 + 6 + 6 = 20,
∴t = 20÷1 = 20;
如答图②,当CP = CB = 6时,作CD⊥AB于点D,则根据面积法求得CD = 4.8,
在Rt△BCD中,由勾股定理得,BD = 3.6,
∴PB = 2BD = 7.2,
∴CA + CB + BP = 8 + 6 + 7.2 = 21.2,
此时t = 21.2÷1 = 21.2;
如答图③,当PC = PB时,作PD⊥BC于点D,作PE⊥AC于点E,则D为BC的中点,可证△APE≌△PBD.
∴AP = BP = $\frac{1}{2}$AB = 5,
∴AC + CB + BP = 8 + 6 + 5 = 19,∴t = 19÷1 = 19.
综上所述,t为20或21.2或19时,△BCP为等腰三角形
