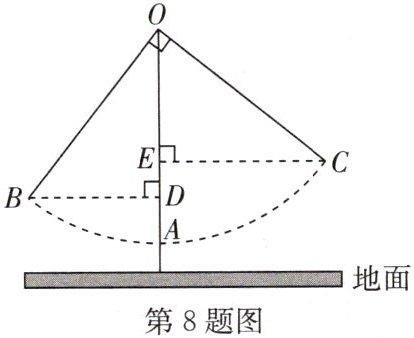
8. 如图,小丽坐在秋千的起始位置$A$处,$OA$与地面垂直,小丽两脚在地面上用力一蹬,妈妈在$B$处接住她后用力一推,爸爸在$C$处接住她。若点$B$距离地面的高度为$1.5m$,点$B$到$OA$的距离$BD$为$1.7m$,点$C$距离地面的高度是$1.6m$,$∠BOC=90^{\circ}$,则点$C$到$OA$的距离$CE$为______
1.8
m。
答案:1.8
9. 如图,在四边形$ABCD$中,$E$为$BC$边的中点。若$AE$平分$∠BAD$,$∠AED=90^{\circ}$,$F$为$AD$上一点,$AF=AB$。
求证:(1)$\triangle ABE≌\triangle AFE$;
(2)$AD=AB+CD$。
证明:(1) ∵AE平分∠BAD,∴∠BAE=∠FAE,
在△ABE和△AFE中,$\left\{\begin{array}{l} AB=AF,\\ ∠BAE=∠FAE,\\ AE=AE,\end{array}\right.$
∴△ABE≌△AFE(
(2) 由(1)知,△ABE≌△AFE,∴EB=EF,∠AEB=∠AEF,∵∠BEC=180°,∠AED=90°,∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,∵点E为BC的中点,∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,$\left\{\begin{array}{l} EC=EF,\\ ∠DEC=∠DEF,\\ ED=ED,\end{array}\right.$
∴△ECD≌△EFD(
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
求证:(1)$\triangle ABE≌\triangle AFE$;
(2)$AD=AB+CD$。
证明:(1) ∵AE平分∠BAD,∴∠BAE=∠FAE,
在△ABE和△AFE中,$\left\{\begin{array}{l} AB=AF,\\ ∠BAE=∠FAE,\\ AE=AE,\end{array}\right.$
∴△ABE≌△AFE(
SAS
).(2) 由(1)知,△ABE≌△AFE,∴EB=EF,∠AEB=∠AEF,∵∠BEC=180°,∠AED=90°,∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,∵点E为BC的中点,∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,$\left\{\begin{array}{l} EC=EF,\\ ∠DEC=∠DEF,\\ ED=ED,\end{array}\right.$
∴△ECD≌△EFD(
SAS
),∴DC=DF,∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
答案:证明:(1) ∵AE平分∠BAD,∴∠BAE=∠FAE,
在△ABE和△AFE中,$\left\{\begin{array}{l} AB=AF,\\ ∠BAE=∠FAE,\\ AE=AE,\end{array}\right.$
∴△ABE≌△AFE(SAS).
(2) 由(1)知,△ABE≌△AFE,∴EB=EF,∠AEB=∠AEF,∵∠BEC=180°,∠AED=90°,∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,∵点E为BC的中点,∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,$\left\{\begin{array}{l} EC=EF,\\ ∠DEC=∠DEF,\\ ED=ED,\end{array}\right.$
∴△ECD≌△EFD(SAS),∴DC=DF,
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
在△ABE和△AFE中,$\left\{\begin{array}{l} AB=AF,\\ ∠BAE=∠FAE,\\ AE=AE,\end{array}\right.$
∴△ABE≌△AFE(SAS).
(2) 由(1)知,△ABE≌△AFE,∴EB=EF,∠AEB=∠AEF,∵∠BEC=180°,∠AED=90°,∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,∵点E为BC的中点,∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,$\left\{\begin{array}{l} EC=EF,\\ ∠DEC=∠DEF,\\ ED=ED,\end{array}\right.$
∴△ECD≌△EFD(SAS),∴DC=DF,
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
10. 如图①,$AB=4cm$,$AC⊥AB$,$BD⊥AB$,$AC=BD=3cm$。点$P$在线段$AB$上以$1cm/s$的速度由点$A$向点$B$运动,同时,点$Q$在线段$BD$上由点$B$向点$D$运动。它们运动的时间为$t s$。
(1)若点$Q$的运动速度与点$P$的运动速度相等,当$t=1$时,$\triangle ACP$与$\triangle BPQ$是否全等?判断此时线段$PC$和线段$PQ$的位置关系,并分别说明理由。
$\triangle ACP$与$\triangle BPQ$
(2)如图②,将(1)中的“$AC⊥AB$,$BD⊥AB$”改为“$∠CAB=∠DBA=60^{\circ}$”,其他条件不变。设点$Q$的运动速度为$x cm/s$,是否存在$x$,使得$\triangle ACP$与$\triangle BPQ$全等?若存在,求出相应的$x$,$t$的值;若不存在,请说明理由。
存在,相应的$x$,$t$的值为
(1)若点$Q$的运动速度与点$P$的运动速度相等,当$t=1$时,$\triangle ACP$与$\triangle BPQ$是否全等?判断此时线段$PC$和线段$PQ$的位置关系,并分别说明理由。
$\triangle ACP$与$\triangle BPQ$
全等
,此时线段$PC$和线段$PQ$的位置关系是垂直
。(2)如图②,将(1)中的“$AC⊥AB$,$BD⊥AB$”改为“$∠CAB=∠DBA=60^{\circ}$”,其他条件不变。设点$Q$的运动速度为$x cm/s$,是否存在$x$,使得$\triangle ACP$与$\triangle BPQ$全等?若存在,求出相应的$x$,$t$的值;若不存在,请说明理由。
存在,相应的$x$,$t$的值为
$\left\{\begin{array}{l} t=1,\\ x=1\end{array}\right.$或$\left\{\begin{array}{l} t=2,\\ x=\frac{3}{2}\end{array}\right.$
。答案:解:(1) △ACP与△BPQ全等,PC⊥PQ. 理由如下:
∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,当t=1时,AP=BQ=1 cm.
∵AB=4 cm,AC=3 cm,∴BP=AB−AP=3 cm=AC.
在△ACP和△BPQ中,$\left\{\begin{array}{l} AP=BQ,\\ ∠A=∠B,\\ AC=BP,\end{array}\right.$
∴△ACP≌△BPQ(SAS),
∴∠ACP=∠BPQ. ∵∠A=90°,∴∠BPQ+∠APC=∠ACP+∠APC=90°,∴∠CPQ=90°,即PC⊥PQ.
(2) ①若△ACP≌△BPQ,则$\left\{\begin{array}{l} AC=BP,\\ AP=BQ,\end{array}\right.$即$\left\{\begin{array}{l} 3=4−t,\\ t=xt,\end{array}\right.$
解得$\left\{\begin{array}{l} t=1,\\ x=1;\end{array}\right.$
②若△ACP≌△BQP,则$\left\{\begin{array}{l} AC=BQ,\\ AP=BP,\end{array}\right.$即$\left\{\begin{array}{l} 3=xt,\\ t=4−t,\end{array}\right.$
解得$\left\{\begin{array}{l} t=2,\\ x=\frac{3}{2}.\end{array}\right.$
综上所述,当$\left\{\begin{array}{l} t=1,\\ x=1\end{array}\right.$或$\left\{\begin{array}{l} t=2,\\ x=\frac{3}{2}\end{array}\right.$时,△ACP与△BPQ全等.
∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,当t=1时,AP=BQ=1 cm.
∵AB=4 cm,AC=3 cm,∴BP=AB−AP=3 cm=AC.
在△ACP和△BPQ中,$\left\{\begin{array}{l} AP=BQ,\\ ∠A=∠B,\\ AC=BP,\end{array}\right.$
∴△ACP≌△BPQ(SAS),
∴∠ACP=∠BPQ. ∵∠A=90°,∴∠BPQ+∠APC=∠ACP+∠APC=90°,∴∠CPQ=90°,即PC⊥PQ.
(2) ①若△ACP≌△BPQ,则$\left\{\begin{array}{l} AC=BP,\\ AP=BQ,\end{array}\right.$即$\left\{\begin{array}{l} 3=4−t,\\ t=xt,\end{array}\right.$
解得$\left\{\begin{array}{l} t=1,\\ x=1;\end{array}\right.$
②若△ACP≌△BQP,则$\left\{\begin{array}{l} AC=BQ,\\ AP=BP,\end{array}\right.$即$\left\{\begin{array}{l} 3=xt,\\ t=4−t,\end{array}\right.$
解得$\left\{\begin{array}{l} t=2,\\ x=\frac{3}{2}.\end{array}\right.$
综上所述,当$\left\{\begin{array}{l} t=1,\\ x=1\end{array}\right.$或$\left\{\begin{array}{l} t=2,\\ x=\frac{3}{2}\end{array}\right.$时,△ACP与△BPQ全等.