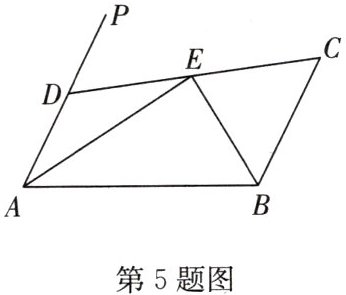
5. 如图,已知 $ AD // BC $,$ \angle PAB $ 的平分线与 $ \angle CBA $ 的平分线相交于点 $ E $,连接 $ CE $ 并延长交 $ AP $ 于点 $ D $。求证:$ AD + BC = AB $。

答案:
证明:如答图,在AB上截取AF=AD,连接EF.
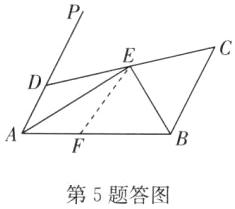
∵AE平分∠PAB,
∴∠DAE=∠FAE.
在△DAE和△FAE中,
{ AD = AF, ∠DAE = ∠FAE, AE = AE }
∴△DAE≌△FAE(SAS),
∴∠AFE=∠ADE.
∵AD//BC,∴∠ADE+∠C=180°.
∵∠AFE+∠EFB=180°,∴∠EFB=∠C,
∵BE平分∠ABC,∴∠EBF=∠EBC.
在△BEF和△BEC中, { ∠EFB = ∠C, ∠EBF = ∠EBC, BE = BE }
∴△BEF≌△BEC(AAS),∴BC=BF.
又AD=AF,∴AD+BC=AF+BF=AB.
证明:如答图,在AB上截取AF=AD,连接EF.

∵AE平分∠PAB,
∴∠DAE=∠FAE.
在△DAE和△FAE中,
{ AD = AF, ∠DAE = ∠FAE, AE = AE }
∴△DAE≌△FAE(SAS),
∴∠AFE=∠ADE.
∵AD//BC,∴∠ADE+∠C=180°.
∵∠AFE+∠EFB=180°,∴∠EFB=∠C,
∵BE平分∠ABC,∴∠EBF=∠EBC.
在△BEF和△BEC中, { ∠EFB = ∠C, ∠EBF = ∠EBC, BE = BE }
∴△BEF≌△BEC(AAS),∴BC=BF.
又AD=AF,∴AD+BC=AF+BF=AB.
6. 如图,在 $ \triangle ABC $ 中,$ \angle ABC = 60^{\circ} $,$ AD $,$ CE $ 分别平分 $ \angle BAC $,$ \angle ACB $,求证:$ AC = AE + CD $。


答案:
证明:如答图,在AC上截取AF=AE,连接OF.

∵AD平分∠BAC,∴∠EAO=∠FAO,
在△AEO与△AFO中, { AE = AF, ∠EAO = ∠FAO, AO = AO }
∴△AEO≌△AFO(SAS),∴∠AOE=∠AOF.
∵AD,CE分别平分∠BAC,∠ACB,
∴$∠ECA+∠DAC = \frac{1}{2}∠ACB + \frac{1}{2}∠BAC = \frac{1}{2}(∠ACB + ∠BAC) = \frac{1}{2}(180°−∠B) = 60°,$则∠AOC=180°−∠ECA−∠DAC=120°,
∴∠AOC=∠DOE=120°,∠AOE=∠COD=∠AOF=60°,
则∠COF=60°,∴∠COD=∠COF,
在△FOC与△DOC中, { ∠COF = ∠COD, CO = CO, ∠FCO = ∠DCO }
∴△FOC≌△DOC(ASA),∴DC=FC,
∵AC=AF+FC,∴AC=AE+CD.
证明:如答图,在AC上截取AF=AE,连接OF.

∵AD平分∠BAC,∴∠EAO=∠FAO,
在△AEO与△AFO中, { AE = AF, ∠EAO = ∠FAO, AO = AO }
∴△AEO≌△AFO(SAS),∴∠AOE=∠AOF.
∵AD,CE分别平分∠BAC,∠ACB,
∴$∠ECA+∠DAC = \frac{1}{2}∠ACB + \frac{1}{2}∠BAC = \frac{1}{2}(∠ACB + ∠BAC) = \frac{1}{2}(180°−∠B) = 60°,$则∠AOC=180°−∠ECA−∠DAC=120°,
∴∠AOC=∠DOE=120°,∠AOE=∠COD=∠AOF=60°,
则∠COF=60°,∴∠COD=∠COF,
在△FOC与△DOC中, { ∠COF = ∠COD, CO = CO, ∠FCO = ∠DCO }
∴△FOC≌△DOC(ASA),∴DC=FC,
∵AC=AF+FC,∴AC=AE+CD.
7. 如图,$ \angle AOB = 90^{\circ} $,$ OC $ 平分 $ \angle AOB $,把含 $ 30^{\circ} $ 角的三角尺的直角顶点放在 $ OC $ 的任意一点 $ P $ 上,并使三角尺的两条直角边分别与 $ OA $,$ OB $ 相交于点 $ E $,$ F $,$ PE $ 与 $ PF $ 相等吗?请你给出证明。


答案:
解:相等. 证明:如答图,过点P作PM⊥OB于点M,PN⊥OA于点N.

∵OC平分∠AOB,
∴∠POM=∠PON,
∵PM⊥OB,PN⊥OA,
∴∠PMO=∠PNO=90°,
在△POM和△PON中,
{ ∠POM = ∠PON, ∠PMO = ∠PNO = 90°, OP = OP }
∴△POM≌△PON(AAS),
∴PM=PN,
∵∠PMO=∠PNO=∠MON=90°,
∴∠MPN=360°−3×90°=90°,
∵∠MPN=∠EPF=90°,∴∠MPF=∠NPE,
在△PMF和△PNE中, { ∠FPM = ∠EPN, PM = PN, ∠PMF = ∠PNE = 90° }
∴△PMF≌△PNE(ASA),∴PF=PE.
解:相等. 证明:如答图,过点P作PM⊥OB于点M,PN⊥OA于点N.

∵OC平分∠AOB,
∴∠POM=∠PON,
∵PM⊥OB,PN⊥OA,
∴∠PMO=∠PNO=90°,
在△POM和△PON中,
{ ∠POM = ∠PON, ∠PMO = ∠PNO = 90°, OP = OP }
∴△POM≌△PON(AAS),
∴PM=PN,
∵∠PMO=∠PNO=∠MON=90°,
∴∠MPN=360°−3×90°=90°,
∵∠MPN=∠EPF=90°,∴∠MPF=∠NPE,
在△PMF和△PNE中, { ∠FPM = ∠EPN, PM = PN, ∠PMF = ∠PNE = 90° }
∴△PMF≌△PNE(ASA),∴PF=PE.
8. 如图,在 $ \triangle ABC $ 中,$ AD $ 平分 $ \angle BAC $,且 $ BD = CD $。求证:$ \angle B = \angle C $。


答案:
证明:如答图,过点D作DE⊥AB于点E,DF⊥AC于点F,∴∠DEA=∠DFA=90°.

∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AD=AD,∠DEA=∠DFA,
∴△ADE≌△ADF(AAS),
∴DE=DF,又BD=CD,
∴Rt△DBE≌Rt△DCF(HL),
∴∠B=∠C.
证明:如答图,过点D作DE⊥AB于点E,DF⊥AC于点F,∴∠DEA=∠DFA=90°.

∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AD=AD,∠DEA=∠DFA,
∴△ADE≌△ADF(AAS),
∴DE=DF,又BD=CD,
∴Rt△DBE≌Rt△DCF(HL),
∴∠B=∠C.