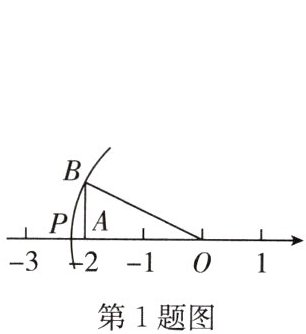
1.(2024·东台期末)如图,数轴上点 A 表示的数是-2,$∠OAB=90^{\circ },AB=1$,以点 O 为圆心,OB 为半径画弧,与数轴的负半轴相交,则交点 P 所表示的数是 (
A.$-\sqrt {2}$
B.$-\sqrt {3}$
C.$-\sqrt {5}$
D.-2.2
C
)
A.$-\sqrt {2}$
B.$-\sqrt {3}$
C.$-\sqrt {5}$
D.-2.2
答案:C
2.如图,一块直角三角形纸片的直角边$AC=6cm,BC=8cm$,现将直角边 AC 沿直线 AD 折叠,使 AC 落在斜边 AB 上,且与 AE 重合,则 CD 等于 (

A.2 cm
B.4 cm
C.3 cm
D.5 cm
A.2 cm
B.4 cm
C.3 cm
D.5 cm
C
)
A.2 cm
B.4 cm
C.3 cm
D.5 cm
A.2 cm
B.4 cm
C.3 cm
D.5 cm
答案:C
3.如图,点 D 在$△ABC$的边 BC 上,若$AB=13,AD=12,BD=5,AC=15$,则 BC 的长为

14
.
答案:14
4.如图,在等腰$△ABC$中,$AB=AC$,D 为 AB 的中点,$BE⊥AC$,垂足为 E.若$DE=\frac {5}{2},BE=3$,则 BC 的长为

$\sqrt{10}$
.
答案:$\sqrt{10}$
5.(2024·镇江期末)如图,$△ABC$中,$AB=AC=5,BC=6$,点 D 是 AB 边上的一个动点,求线段 CD 长度的最小值.


答案:
解:如答图,过点A作AH⊥BC于点H.

∵AB = AC = 5,BC = 6,∴BH = CH = $\frac{1}{2}$BC = 3,
∴AH = $\sqrt{AB^2 - BH^2}$ = $\sqrt{5^2 - 3^2}$ = 4.
由垂线段最短可知,当CD⊥AB时,线段CD最短,
此时$\frac{1}{2}$AB·CD = $\frac{1}{2}$BC·AH,
∴CD = $\frac{24}{5}$.
∴线段CD长度的最小值为$\frac{24}{5}$.
解:如答图,过点A作AH⊥BC于点H.

∵AB = AC = 5,BC = 6,∴BH = CH = $\frac{1}{2}$BC = 3,
∴AH = $\sqrt{AB^2 - BH^2}$ = $\sqrt{5^2 - 3^2}$ = 4.
由垂线段最短可知,当CD⊥AB时,线段CD最短,
此时$\frac{1}{2}$AB·CD = $\frac{1}{2}$BC·AH,
∴CD = $\frac{24}{5}$.
∴线段CD长度的最小值为$\frac{24}{5}$.
6.(2024春·启东校级月考)在$Rt△ABC$中,$AB=5,AC=4$,则$BC=$ (
A.3
B.1
C.$\sqrt {41}$
D.$\sqrt {41}$或3
D
)A.3
B.1
C.$\sqrt {41}$
D.$\sqrt {41}$或3
答案:D
7.如图,直线 l 过正方形 ABCD 的顶点 B,点 A,C 到直线 l 的距离分别是 3 和 4,则正方形的边长是 (

A.5
B.3
C.$\sqrt {5}$
D.$\sqrt {3}$
A
)
A.5
B.3
C.$\sqrt {5}$
D.$\sqrt {3}$
答案:A