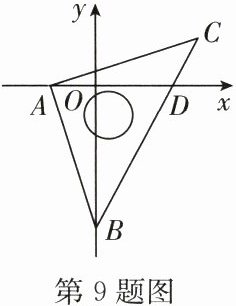
9.(2024·苏州期末)如图,将一块含$45^{\circ }$角的直角三角板放在平面直角坐标系中,顶点$A$,$B分别在x$轴、$y$轴上,斜边$BC与x轴交于点D$.已知$∠ABC= 45^{\circ }$,点$A的坐标为(-\frac {4}{3},0)$,点$B的坐标为(0,-4)$,则点$D$的坐标为____.
答案：(2,0)
解析：
解：设点$C$的坐标为$(x,y)$。
因为$\angle ABC = 45^\circ$，$\triangle ABC$是含$45^\circ$角的直角三角板，点$B$在$y$轴上，点$A$在$x$轴上，所以$\angle BAC = 90^\circ$（或$\angle BCA = 90^\circ$，此处根据图形及后续计算判断为$\angle BAC = 90^\circ$）。
$\overrightarrow{AB}=(0 - (-\frac{4}{3}), -4 - 0)=(\frac{4}{3}, -4)$，$\overrightarrow{AC}=(x - (-\frac{4}{3}), y - 0)=(x + \frac{4}{3}, y)$。
因为$\angle BAC = 90^\circ$，所以$\overrightarrow{AB} \cdot \overrightarrow{AC} = 0$，即$\frac{4}{3}(x + \frac{4}{3}) + (-4)y = 0$，化简得$x + \frac{4}{3} - 3y = 0$，即$x = 3y - \frac{4}{3}$。
又因为$\triangle ABC$是等腰直角三角形，$AB = AC$（或$AB = BC$，根据$\angle ABC = 45^\circ$，若$\angle BAC = 90^\circ$，则$AB = AC$）。
$AB = \sqrt{(\frac{4}{3})^2 + (-4)^2} = \sqrt{\frac{16}{9} + 16} = \sqrt{\frac{160}{9}} = \frac{4\sqrt{10}}{3}$。
$AC = \sqrt{(x + \frac{4}{3})^2 + y^2} = \frac{4\sqrt{10}}{3}$，将$x = 3y - \frac{4}{3}$代入得：
$\sqrt{(3y - \frac{4}{3} + \frac{4}{3})^2 + y^2} = \frac{4\sqrt{10}}{3}$，即$\sqrt{(3y)^2 + y^2} = \frac{4\sqrt{10}}{3}$，$\sqrt{10y^2} = \frac{4\sqrt{10}}{3}$，$|y|\sqrt{10} = \frac{4\sqrt{10}}{3}$，解得$|y| = \frac{4}{3}$。
因为点$C$在第一象限（根据图形），所以$y = \frac{4}{3}$，则$x = 3×\frac{4}{3} - \frac{4}{3} = 4 - \frac{4}{3} = \frac{8}{3}$，所以$C(\frac{8}{3}, \frac{4}{3})$。
设直线$BC$的解析式为$y = kx + b$，将$B(0, -4)$，$C(\frac{8}{3}, \frac{4}{3})$代入得：
$\begin{cases}b = -4\\frac{8}{3}k + b = \frac{4}{3}\end{cases}$，将$b = -4$代入第二式得$\frac{8}{3}k - 4 = \frac{4}{3}$，$\frac{8}{3}k = \frac{16}{3}$，$k = 2$，所以直线$BC$：$y = 2x - 4$。
令$y = 0$，则$2x - 4 = 0$，$x = 2$，所以点$D$的坐标为$(2,0)$。
答案：$(2,0)$
因为$\angle ABC = 45^\circ$，$\triangle ABC$是含$45^\circ$角的直角三角板，点$B$在$y$轴上，点$A$在$x$轴上，所以$\angle BAC = 90^\circ$（或$\angle BCA = 90^\circ$，此处根据图形及后续计算判断为$\angle BAC = 90^\circ$）。
$\overrightarrow{AB}=(0 - (-\frac{4}{3}), -4 - 0)=(\frac{4}{3}, -4)$，$\overrightarrow{AC}=(x - (-\frac{4}{3}), y - 0)=(x + \frac{4}{3}, y)$。
因为$\angle BAC = 90^\circ$，所以$\overrightarrow{AB} \cdot \overrightarrow{AC} = 0$，即$\frac{4}{3}(x + \frac{4}{3}) + (-4)y = 0$，化简得$x + \frac{4}{3} - 3y = 0$，即$x = 3y - \frac{4}{3}$。
又因为$\triangle ABC$是等腰直角三角形，$AB = AC$（或$AB = BC$，根据$\angle ABC = 45^\circ$，若$\angle BAC = 90^\circ$，则$AB = AC$）。
$AB = \sqrt{(\frac{4}{3})^2 + (-4)^2} = \sqrt{\frac{16}{9} + 16} = \sqrt{\frac{160}{9}} = \frac{4\sqrt{10}}{3}$。
$AC = \sqrt{(x + \frac{4}{3})^2 + y^2} = \frac{4\sqrt{10}}{3}$，将$x = 3y - \frac{4}{3}$代入得：
$\sqrt{(3y - \frac{4}{3} + \frac{4}{3})^2 + y^2} = \frac{4\sqrt{10}}{3}$，即$\sqrt{(3y)^2 + y^2} = \frac{4\sqrt{10}}{3}$，$\sqrt{10y^2} = \frac{4\sqrt{10}}{3}$，$|y|\sqrt{10} = \frac{4\sqrt{10}}{3}$，解得$|y| = \frac{4}{3}$。
因为点$C$在第一象限（根据图形），所以$y = \frac{4}{3}$，则$x = 3×\frac{4}{3} - \frac{4}{3} = 4 - \frac{4}{3} = \frac{8}{3}$，所以$C(\frac{8}{3}, \frac{4}{3})$。
设直线$BC$的解析式为$y = kx + b$，将$B(0, -4)$，$C(\frac{8}{3}, \frac{4}{3})$代入得：
$\begin{cases}b = -4\\frac{8}{3}k + b = \frac{4}{3}\end{cases}$，将$b = -4$代入第二式得$\frac{8}{3}k - 4 = \frac{4}{3}$，$\frac{8}{3}k = \frac{16}{3}$，$k = 2$，所以直线$BC$：$y = 2x - 4$。
令$y = 0$，则$2x - 4 = 0$，$x = 2$，所以点$D$的坐标为$(2,0)$。
答案：$(2,0)$
10.(12分)(2024·苏州期末)如图,在$7×7$的网格中,每个小正方形的边长为1,小正方形的顶点叫作格点,点$A$,$B$,$C$均为格点.
(1)线段$AB$的长为____;
(2)确定格点$D$,使$\triangle ACD$为等腰直角三角形,画出所有符合条件的点$D$.
(1)线段$AB$的长为____;
(2)确定格点$D$,使$\triangle ACD$为等腰直角三角形,画出所有符合条件的点$D$.
答案：
(1)5 (2)解:如答图,点$D_1,D_2,D_3,D_4,D_5$均满足题意.
(1)5 (2)解:如答图,点$D_1,D_2,D_3,D_4,D_5$均满足题意.
11.(16分)如图,在平面直角坐标系中,每个小正方形的边长都是1.
(1)按要求作图:作$\triangle ABC关于y轴对称的\triangle A_{1}B_{1}C_{1}$;
(2)将点$A$先向上平移3个单位长度,再向右平移8个单位长度得到点$A_{2}$,则点$A_{2}$的坐标为____;
(3)$\triangle ABC$的面积为____;
(4)若$Q为x$轴上一点,连接$AQ$,$BQ$,求$\triangle ABQ$周长的最小值.
(1)按要求作图:作$\triangle ABC关于y轴对称的\triangle A_{1}B_{1}C_{1}$;
(2)将点$A$先向上平移3个单位长度,再向右平移8个单位长度得到点$A_{2}$,则点$A_{2}$的坐标为____;
(3)$\triangle ABC$的面积为____;
(4)若$Q为x$轴上一点,连接$AQ$,$BQ$,求$\triangle ABQ$周长的最小值.
答案：
(1)解:如答图,$\triangle A_1B_1C_1$即为所求.
(2)(3,2) (3)$\frac{23}{2}$ (4)解:如答图,作点$A$关于$x$轴的对称点$A'$,连接$A'B$交$x$轴于点$Q$,则$AQ + BQ$的最小值为$A'B$的长.由图可得,$AB = \sqrt{2^2 + 3^2} = \sqrt{13}$,$A'B = \sqrt{3^2 + 4^2} = 5$,此时$\triangle ABQ$的周长$= AQ + BQ + AB = A'B + AB = 5 + \sqrt{13}$,$\therefore \triangle ABQ$周长的最小值为$5 + \sqrt{13}$.
(1)解:如答图,$\triangle A_1B_1C_1$即为所求.
(2)(3,2) (3)$\frac{23}{2}$ (4)解:如答图,作点$A$关于$x$轴的对称点$A'$,连接$A'B$交$x$轴于点$Q$,则$AQ + BQ$的最小值为$A'B$的长.由图可得,$AB = \sqrt{2^2 + 3^2} = \sqrt{13}$,$A'B = \sqrt{3^2 + 4^2} = 5$,此时$\triangle ABQ$的周长$= AQ + BQ + AB = A'B + AB = 5 + \sqrt{13}$,$\therefore \triangle ABQ$周长的最小值为$5 + \sqrt{13}$.12.(18分)已知$\triangle ABC$中,$AB= AC$.
(1)如图①,在$\triangle ADE$中,$AD= AE$,连接$BD$,$CE$,若$∠DAE= ∠BAC$,求证:$BD= CE$;
(2)如图②,在$\triangle ADE$中,$AD= AE$,连接$BE$,$CE$,若$∠DAE= ∠BAC= 60^{\circ }$,$CE⊥AD于点F$,$AE= 4$,$AC= \sqrt {7}$,求$BE$的长;
(3)如图③,在$\triangle BCD$中,$∠CBD= ∠CDB= 45^{\circ }$,连接$AD$,若$∠CAB= 45^{\circ }$,求$\frac {AD}{AB}$的值.
(1)如图①,在$\triangle ADE$中,$AD= AE$,连接$BD$,$CE$,若$∠DAE= ∠BAC$,求证:$BD= CE$;
(2)如图②,在$\triangle ADE$中,$AD= AE$,连接$BE$,$CE$,若$∠DAE= ∠BAC= 60^{\circ }$,$CE⊥AD于点F$,$AE= 4$,$AC= \sqrt {7}$,求$BE$的长;
(3)如图③,在$\triangle BCD$中,$∠CBD= ∠CDB= 45^{\circ }$,连接$AD$,若$∠CAB= 45^{\circ }$,求$\frac {AD}{AB}$的值.
答案：
(1)证明:$\because \angle DAE = \angle BAC$,$\therefore \angle EAC = \angle DAB$,$\because AE = AD$,$AC = AB$,$\therefore \triangle EAC \cong \triangle DAB (SAS)$,$\therefore EC = BD$. (2)解:如答图①,连接$BD$.
$\because AE = AD$,$\angle EAD = 60^{\circ}$,$\therefore \triangle AED$是等边三角形,$\therefore \angle DEA = \angle ADE = 60^{\circ}$,$\because EF \perp AD$,$\therefore \angle FEA = \frac{1}{2}\angle DEA = 30^{\circ}$,$\therefore AF = \frac{1}{2}AE = 2$.$\because \angle DAE = \angle BAC$,$\therefore \angle EAC = \angle DAB$,$\because AE = AD$,$AC = AB$,$\therefore \triangle EAC \cong \triangle DAB (SAS)$,$\therefore \angle BDA = \angle AEC = 30^{\circ}$,$EC = BD$,$\therefore \angle EDB = \angle EDA + \angle BDA = 90^{\circ}$.$\because AE = 4$,$AF = 2$,$AC = \sqrt{7}$,$\angle EFA = \angle AFC = 90^{\circ}$,$\therefore EF = \sqrt{AE^2 - AF^2} = \sqrt{4^2 - 2^2} = 2\sqrt{3}$,$CF = \sqrt{AC^2 - AF^2} = \sqrt{7 - 4} = \sqrt{3}$,$\therefore EC = BD = 3\sqrt{3}$,$\therefore BE = \sqrt{DE^2 + BD^2} = \sqrt{4^2 + (3\sqrt{3})^2} = \sqrt{43}$. (3)解:如答图②,作$CM \perp CA$,使得$CM = CA$,连接$AM$,$BM$.$\because CA = CM$,$\angle ACM = 90^{\circ}$,$\therefore \angle CAM = 45^{\circ}$,$\because \angle CAB = 45^{\circ}$,$\therefore \angle MAB = 45^{\circ} + 45^{\circ} = 90^{\circ}$.设$AB = AC = m$,则$AM = \sqrt{2}m$,$BM = \sqrt{AM^2 + AB^2} = \sqrt{3}m$,$\because \angle ACM = \angle BCD = 90^{\circ}$,$\therefore \angle BCM = \angle ACD$,$\because CA = CM$,$CB = CD$,$\therefore \triangle ACD \cong \triangle MCB (SAS)$,$\therefore AD = BM = \sqrt{3}m$,$\therefore \frac{AD}{AB} = \frac{\sqrt{3}m}{m} = \sqrt{3}$.
(1)证明:$\because \angle DAE = \angle BAC$,$\therefore \angle EAC = \angle DAB$,$\because AE = AD$,$AC = AB$,$\therefore \triangle EAC \cong \triangle DAB (SAS)$,$\therefore EC = BD$. (2)解:如答图①,连接$BD$.
$\because AE = AD$,$\angle EAD = 60^{\circ}$,$\therefore \triangle AED$是等边三角形,$\therefore \angle DEA = \angle ADE = 60^{\circ}$,$\because EF \perp AD$,$\therefore \angle FEA = \frac{1}{2}\angle DEA = 30^{\circ}$,$\therefore AF = \frac{1}{2}AE = 2$.$\because \angle DAE = \angle BAC$,$\therefore \angle EAC = \angle DAB$,$\because AE = AD$,$AC = AB$,$\therefore \triangle EAC \cong \triangle DAB (SAS)$,$\therefore \angle BDA = \angle AEC = 30^{\circ}$,$EC = BD$,$\therefore \angle EDB = \angle EDA + \angle BDA = 90^{\circ}$.$\because AE = 4$,$AF = 2$,$AC = \sqrt{7}$,$\angle EFA = \angle AFC = 90^{\circ}$,$\therefore EF = \sqrt{AE^2 - AF^2} = \sqrt{4^2 - 2^2} = 2\sqrt{3}$,$CF = \sqrt{AC^2 - AF^2} = \sqrt{7 - 4} = \sqrt{3}$,$\therefore EC = BD = 3\sqrt{3}$,$\therefore BE = \sqrt{DE^2 + BD^2} = \sqrt{4^2 + (3\sqrt{3})^2} = \sqrt{43}$. (3)解:如答图②,作$CM \perp CA$,使得$CM = CA$,连接$AM$,$BM$.$\because CA = CM$,$\angle ACM = 90^{\circ}$,$\therefore \angle CAM = 45^{\circ}$,$\because \angle CAB = 45^{\circ}$,$\therefore \angle MAB = 45^{\circ} + 45^{\circ} = 90^{\circ}$.设$AB = AC = m$,则$AM = \sqrt{2}m$,$BM = \sqrt{AM^2 + AB^2} = \sqrt{3}m$,$\because \angle ACM = \angle BCD = 90^{\circ}$,$\therefore \angle BCM = \angle ACD$,$\because CA = CM$,$CB = CD$,$\therefore \triangle ACD \cong \triangle MCB (SAS)$,$\therefore AD = BM = \sqrt{3}m$,$\therefore \frac{AD}{AB} = \frac{\sqrt{3}m}{m} = \sqrt{3}$.