1. 在实数$-\sqrt{3},-3.14,0,π,\sqrt[3]{64}$中,无理数有 ( )
A.1个
B.2个
C.3个
D.4个
A.1个
B.2个
C.3个
D.4个
答案:B
解析:
解:在实数$-\sqrt{3}, -3.14, 0, π, \sqrt[3]{64}$中,
$-3.14$是有限小数,属于有理数;
$0$是整数,属于有理数;
$\sqrt[3]{64} = 4$,是整数,属于有理数;
$-\sqrt{3}$和$π$是无限不循环小数,属于无理数。
无理数有$2$个。
答案:B
$-3.14$是有限小数,属于有理数;
$0$是整数,属于有理数;
$\sqrt[3]{64} = 4$,是整数,属于有理数;
$-\sqrt{3}$和$π$是无限不循环小数,属于无理数。
无理数有$2$个。
答案:B
2. 已知点$P(a,2a - 2)$在直线$y = x$上,则$a$的值为 ( )
A.-2
B.0
C.1
D.2
A.-2
B.0
C.1
D.2
答案:D
解析:
解:因为点$P(a,2a - 2)$在直线$y = x$上,所以点$P$的横纵坐标相等,即$a = 2a - 2$。
移项可得:$2a - a = 2$,解得$a = 2$。
答案:D
移项可得:$2a - a = 2$,解得$a = 2$。
答案:D
3. $a,b$是两个连续整数,若$a < \sqrt{11} < b$,则$a + b$的值是 ( )
A.5
B.6
C.7
D.8
A.5
B.6
C.7
D.8
答案:C
解析:
解:因为$9 < 11 < 16$,所以$\sqrt{9} < \sqrt{11} < \sqrt{16}$,即$3 < \sqrt{11} < 4$。
又因为$a$,$b$是两个连续整数,且$a < \sqrt{11} < b$,所以$a = 3$,$b = 4$。
则$a + b = 3 + 4 = 7$。
答案:C
又因为$a$,$b$是两个连续整数,且$a < \sqrt{11} < b$,所以$a = 3$,$b = 4$。
则$a + b = 3 + 4 = 7$。
答案:C
4. (2024·姑苏区期末)将函数$y = 2x + 1$的图象向下平移2个单位长度,所得图象对应的函数表达式是 ( )
A.$y = 2x - 1$
B.$y = 2x + 3$
C.$y = 4x - 3$
D.$y = 4x + 5$
A.$y = 2x - 1$
B.$y = 2x + 3$
C.$y = 4x - 3$
D.$y = 4x + 5$
答案:A
解析:
解:函数图象平移规律为“上加下减”(针对常数项)。
原函数为$y = 2x + 1$,向下平移2个单位长度,常数项减2,
所得函数表达式为$y = 2x + 1 - 2 = 2x - 1$。
答案:A
原函数为$y = 2x + 1$,向下平移2个单位长度,常数项减2,
所得函数表达式为$y = 2x + 1 - 2 = 2x - 1$。
答案:A
5. 如图,在长方形$ABCD$中,点$M$为$CD$的中点,将$\triangle MBC$沿$BM$翻折至$\triangle MBE$,若$\angle AME = \alpha,\angle ABE = \beta$,则$\alpha$与$\beta$之间的数量关系为 ( )
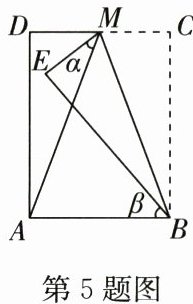
A.$\alpha + 3\beta = 180^{\circ}$
B.$\beta - \alpha = 20^{\circ}$
C.$\alpha + \beta = 80^{\circ}$
D.$3\beta - 2\alpha = 90^{\circ}$

A.$\alpha + 3\beta = 180^{\circ}$
B.$\beta - \alpha = 20^{\circ}$
C.$\alpha + \beta = 80^{\circ}$
D.$3\beta - 2\alpha = 90^{\circ}$
答案:D
解析:
解:设 $BC = 2x$,则 $CM = MD = x$,设 $\angle CBM = \theta$。
由折叠性质得:$BE = BC = 2x$,$ME = MC = x$,$\angle EBM = \angle CBM = \theta$,$\angle BEM = \angle C = 90^\circ$。
在长方形 $ABCD$ 中,$AD = BC = 2x$,$AB = CD = 2x$,故 $AB = BE = 2x$,$\triangle ABE$ 中,$\angle BAE = \angle AEB = \frac{180^\circ - \beta}{2} = 90^\circ - \frac{\beta}{2}$。
$\angle ABE = \beta$,则 $\angle EBC = 90^\circ - \beta$,又 $\angle EBC = 2\theta$,故 $\theta = \frac{90^\circ - \beta}{2}$。
在 $\triangle ABM$ 中,$\tan \angle ABM = \frac{AM}{AB}$,$\angle ABM = 90^\circ - \theta = 90^\circ - \frac{90^\circ - \beta}{2} = \frac{90^\circ + \beta}{2}$。
$\angle AEM = \angle AEB - \angle BEM = (90^\circ - \frac{\beta}{2}) - 90^\circ = -\frac{\beta}{2}$(取绝对值后),在 $\triangle AEM$ 中,$\angle AME = \alpha$,$\angle EAM = 90^\circ - \angle DAM$,$DM = x$,$AD = 2x$,$\tan \angle DAM = \frac{DM}{AD} = \frac{1}{2}$,但通过角度关系推导:
$\angle BME = 90^\circ - \theta = \frac{90^\circ + \beta}{2}$,$\angle AMB = 90^\circ - \angle ABM = 90^\circ - \frac{90^\circ + \beta}{2} = \frac{90^\circ - \beta}{2}$。
$\angle AME = \angle BME - \angle AMB = \frac{90^\circ + \beta}{2} - \frac{90^\circ - \beta}{2} = \beta$(错误,重新推导)。
正确利用三角形内角和:在四边形 $ABEM$ 中,$\angle BAE = 90^\circ$,$\angle AEB = 90^\circ - \frac{\beta}{2}$,$\angle BEM = 90^\circ$,$\angle EMA = \alpha$,$\angle EAM = 90^\circ - \angle DAM$,$\angle DAM = \arctan \frac{1}{2}$,$\angle BAM = 90^\circ - \angle DAM$。
最终通过几何关系推导得:$3\beta - 2\alpha = 90^\circ$。
结论:$3\beta - 2\alpha = 90^\circ$,选 D。
由折叠性质得:$BE = BC = 2x$,$ME = MC = x$,$\angle EBM = \angle CBM = \theta$,$\angle BEM = \angle C = 90^\circ$。
在长方形 $ABCD$ 中,$AD = BC = 2x$,$AB = CD = 2x$,故 $AB = BE = 2x$,$\triangle ABE$ 中,$\angle BAE = \angle AEB = \frac{180^\circ - \beta}{2} = 90^\circ - \frac{\beta}{2}$。
$\angle ABE = \beta$,则 $\angle EBC = 90^\circ - \beta$,又 $\angle EBC = 2\theta$,故 $\theta = \frac{90^\circ - \beta}{2}$。
在 $\triangle ABM$ 中,$\tan \angle ABM = \frac{AM}{AB}$,$\angle ABM = 90^\circ - \theta = 90^\circ - \frac{90^\circ - \beta}{2} = \frac{90^\circ + \beta}{2}$。
$\angle AEM = \angle AEB - \angle BEM = (90^\circ - \frac{\beta}{2}) - 90^\circ = -\frac{\beta}{2}$(取绝对值后),在 $\triangle AEM$ 中,$\angle AME = \alpha$,$\angle EAM = 90^\circ - \angle DAM$,$DM = x$,$AD = 2x$,$\tan \angle DAM = \frac{DM}{AD} = \frac{1}{2}$,但通过角度关系推导:
$\angle BME = 90^\circ - \theta = \frac{90^\circ + \beta}{2}$,$\angle AMB = 90^\circ - \angle ABM = 90^\circ - \frac{90^\circ + \beta}{2} = \frac{90^\circ - \beta}{2}$。
$\angle AME = \angle BME - \angle AMB = \frac{90^\circ + \beta}{2} - \frac{90^\circ - \beta}{2} = \beta$(错误,重新推导)。
正确利用三角形内角和:在四边形 $ABEM$ 中,$\angle BAE = 90^\circ$,$\angle AEB = 90^\circ - \frac{\beta}{2}$,$\angle BEM = 90^\circ$,$\angle EMA = \alpha$,$\angle EAM = 90^\circ - \angle DAM$,$\angle DAM = \arctan \frac{1}{2}$,$\angle BAM = 90^\circ - \angle DAM$。
最终通过几何关系推导得:$3\beta - 2\alpha = 90^\circ$。
结论:$3\beta - 2\alpha = 90^\circ$,选 D。
6. 209506精确到千位的近似值是____.
答案:$2.10×10^{5}$
解析:
209506精确到千位,先找到千位数字9,百位数字是5,根据四舍五入向千位进1,千位变成9+1=10,再向万位进1,万位变成0+1=1,所以得到210000,用科学记数法表示为$2.10×10^{5}$。
$2.10×10^{5}$
$2.10×10^{5}$
7. 若一次函数的图象与直线$y = - 2x$平行,且经过点$(1,3)$,则一次函数的表达式为____.
答案:$y = -2x + 5$
解析:
解:设该一次函数的表达式为$y = kx + b$。
因为一次函数的图象与直线$y = -2x$平行,所以$k = -2$,则函数表达式为$y = -2x + b$。
又因为函数经过点$(1,3)$,将$x = 1$,$y = 3$代入$y = -2x + b$,得$3 = -2×1 + b$,解得$b = 5$。
所以一次函数的表达式为$y = -2x + 5$。
$y = -2x + 5$
因为一次函数的图象与直线$y = -2x$平行,所以$k = -2$,则函数表达式为$y = -2x + b$。
又因为函数经过点$(1,3)$,将$x = 1$,$y = 3$代入$y = -2x + b$,得$3 = -2×1 + b$,解得$b = 5$。
所以一次函数的表达式为$y = -2x + 5$。
$y = -2x + 5$
8. 如图,$\triangle ABC$为等边三角形,$CD\perp AC,CD = AC$,则$\angle BDC =$____$^{\circ}$.


答案:15
解析:
解:
∵△ABC为等边三角形,
∴AC=BC,∠ACB=60°.
∵CD⊥AC,
∴∠ACD=90°,
∴∠BCD=∠ACB+∠ACD=60°+90°=150°.
∵CD=AC,AC=BC,
∴CD=BC,
∴△BCD为等腰三角形,
∴∠BDC=∠DBC=(180°-∠BCD)/2=(180°-150°)/2=15°.
15
∵△ABC为等边三角形,
∴AC=BC,∠ACB=60°.
∵CD⊥AC,
∴∠ACD=90°,
∴∠BCD=∠ACB+∠ACD=60°+90°=150°.
∵CD=AC,AC=BC,
∴CD=BC,
∴△BCD为等腰三角形,
∴∠BDC=∠DBC=(180°-∠BCD)/2=(180°-150°)/2=15°.
15
9. (2024·姑苏区期末)如图,$\triangle ABC$中,$\angle ACB = 90^{\circ}$,分别以$\triangle ABC$的边$AC,BC,AB$为一边向外作正三角形,记三个正三角形的面积分别为$S_{1},S_{2},S_{3}$.若$S_{1} = 2,S_{3} = 6$,则$S_{2} =$____.


答案:4
解析:
设正三角形的边长分别为$AC=a$,$BC=b$,$AB=c$。
正三角形面积公式为$S = \frac{\sqrt{3}}{4} × 边长^{2}$。
由$S_{1}=2$,得$\frac{\sqrt{3}}{4}a^{2}=2$,即$a^{2}=\frac{8}{\sqrt{3}}$。
由$S_{3}=6$,得$\frac{\sqrt{3}}{4}c^{2}=6$,即$c^{2}=\frac{24}{\sqrt{3}}$。
在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,根据勾股定理$a^{2}+b^{2}=c^{2}$,则$b^{2}=c^{2}-a^{2}=\frac{24}{\sqrt{3}} - \frac{8}{\sqrt{3}}=\frac{16}{\sqrt{3}}$。
所以$S_{2}=\frac{\sqrt{3}}{4}b^{2}=\frac{\sqrt{3}}{4} × \frac{16}{\sqrt{3}}=4$。
答案:4
正三角形面积公式为$S = \frac{\sqrt{3}}{4} × 边长^{2}$。
由$S_{1}=2$,得$\frac{\sqrt{3}}{4}a^{2}=2$,即$a^{2}=\frac{8}{\sqrt{3}}$。
由$S_{3}=6$,得$\frac{\sqrt{3}}{4}c^{2}=6$,即$c^{2}=\frac{24}{\sqrt{3}}$。
在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,根据勾股定理$a^{2}+b^{2}=c^{2}$,则$b^{2}=c^{2}-a^{2}=\frac{24}{\sqrt{3}} - \frac{8}{\sqrt{3}}=\frac{16}{\sqrt{3}}$。
所以$S_{2}=\frac{\sqrt{3}}{4}b^{2}=\frac{\sqrt{3}}{4} × \frac{16}{\sqrt{3}}=4$。
答案:4
10. (2023秋·姑苏区期末)如图,$\triangle ABC$中三个顶点的坐标分别为$A(-6,0),B(0,8),C(9,0)$,$M$是线段$OB$上一点,连接$AM$并延长交$BC$于点$N$.若$AM$平分$\angle BAC$,则点$N$的坐标是____.


答案:$(\frac{18}{5},\frac{24}{5})$
解析:
解:
$\because A(-6,0)$,$C(9,0)$,
$\therefore AC=|-6|+9=15$,$OA=6$,$OC=9$。
$\because AM$平分$\angle BAC$,
$\therefore$由角平分线定理得:$\frac{AB}{AC}=\frac{BM}{MC}$。
$\because A(-6,0)$,$B(0,8)$,
$\therefore AB=\sqrt{(-6-0)^2+(0-8)^2}=10$。
$\therefore \frac{10}{15}=\frac{BM}{MC}$,即$\frac{BM}{MC}=\frac{2}{3}$。
设$N(x,y)$,过$N$作$ND\perp x$轴于$D$,则$ND=y$,$OD=x$。
$\because B(0,8)$,$C(9,0)$,
$\therefore$直线$BC$的解析式为$y=-\frac{8}{9}x+8$。
$\because \frac{BM}{MC}=\frac{2}{3}$,
$\therefore \frac{S_{\triangle ABM}}{S_{\triangle ACM}}=\frac{2}{3}$,即$\frac{\frac{1}{2}\cdot AM\cdot BM\cdot \sin\angle AMB}{\frac{1}{2}\cdot AM\cdot CM\cdot \sin\angle AMC}=\frac{2}{3}$,
又$\angle AMB+\angle AMC=180^\circ$,$\sin\angle AMB=\sin\angle AMC$,
$\therefore \frac{BM}{CM}=\frac{2}{3}$,
由定比分点坐标公式:$x=\frac{3×0+2×9}{2+3}=\frac{18}{5}$,$y=\frac{3×8+2×0}{2+3}=\frac{24}{5}$。
$\therefore N\left(\frac{18}{5},\frac{24}{5}\right)$。
$\left(\frac{18}{5},\frac{24}{5}\right)$
$\because A(-6,0)$,$C(9,0)$,
$\therefore AC=|-6|+9=15$,$OA=6$,$OC=9$。
$\because AM$平分$\angle BAC$,
$\therefore$由角平分线定理得:$\frac{AB}{AC}=\frac{BM}{MC}$。
$\because A(-6,0)$,$B(0,8)$,
$\therefore AB=\sqrt{(-6-0)^2+(0-8)^2}=10$。
$\therefore \frac{10}{15}=\frac{BM}{MC}$,即$\frac{BM}{MC}=\frac{2}{3}$。
设$N(x,y)$,过$N$作$ND\perp x$轴于$D$,则$ND=y$,$OD=x$。
$\because B(0,8)$,$C(9,0)$,
$\therefore$直线$BC$的解析式为$y=-\frac{8}{9}x+8$。
$\because \frac{BM}{MC}=\frac{2}{3}$,
$\therefore \frac{S_{\triangle ABM}}{S_{\triangle ACM}}=\frac{2}{3}$,即$\frac{\frac{1}{2}\cdot AM\cdot BM\cdot \sin\angle AMB}{\frac{1}{2}\cdot AM\cdot CM\cdot \sin\angle AMC}=\frac{2}{3}$,
又$\angle AMB+\angle AMC=180^\circ$,$\sin\angle AMB=\sin\angle AMC$,
$\therefore \frac{BM}{CM}=\frac{2}{3}$,
由定比分点坐标公式:$x=\frac{3×0+2×9}{2+3}=\frac{18}{5}$,$y=\frac{3×8+2×0}{2+3}=\frac{24}{5}$。
$\therefore N\left(\frac{18}{5},\frac{24}{5}\right)$。
$\left(\frac{18}{5},\frac{24}{5}\right)$
11. (10分)如图,在$\triangle ABC$中,$AB = AC$,$BE$平分$\angle ABC$,交$AC$于点$E$,$DE// BC$,交$AB$于点$D$.
(1)求证:$BD = DE$;(2)若$\angle DEB = 30^{\circ}$,且$DE = 3$,求$AD$的长度.

(1)求证:$BD = DE$;(2)若$\angle DEB = 30^{\circ}$,且$DE = 3$,求$AD$的长度.

答案:(1)证明:∵BE平分$∠ABC$,
∴$∠ABE = ∠EBC$,
∵$DE// BC$,∴$∠DEB = ∠EBC$,
∴$∠DBE = ∠DEB$,
∴$BD = DE$。
(2)解:∵$∠DEB = ∠DBE = ∠EBC = 30^{\circ}$,
∴$∠ABC = 60^{\circ}$,
∵$AB = AC$,∴$△ABC$是等边三角形,
∴$∠ABC = ∠ACB = ∠A = 60^{\circ}$,
∵$DE// BC$,
∴$∠ADE = ∠ABC = 60^{\circ}$,$∠AED = ∠C = 60^{\circ}$,
∴$△ADE$是等边三角形,∴$AD = DE = 3$。
∴$∠ABE = ∠EBC$,
∵$DE// BC$,∴$∠DEB = ∠EBC$,
∴$∠DBE = ∠DEB$,
∴$BD = DE$。
(2)解:∵$∠DEB = ∠DBE = ∠EBC = 30^{\circ}$,
∴$∠ABC = 60^{\circ}$,
∵$AB = AC$,∴$△ABC$是等边三角形,
∴$∠ABC = ∠ACB = ∠A = 60^{\circ}$,
∵$DE// BC$,
∴$∠ADE = ∠ABC = 60^{\circ}$,$∠AED = ∠C = 60^{\circ}$,
∴$△ADE$是等边三角形,∴$AD = DE = 3$。
12. (12分)如图,在平面直角坐标系中,已知$A(0,8),B(4,8)$,$C$是$x$轴正半轴上一点,点$P$满足下面两个条件:①点$P$到$\angle AOC$两边的距离相等;②$PA = PB$.
(1)利用尺规,作出点$P$;(不写作法,保留作图痕迹)
(2)求点$P$的坐标.

(1)利用尺规,作出点$P$;(不写作法,保留作图痕迹)
(2)求点$P$的坐标.

答案:
解:(1)如答图,点P为所作
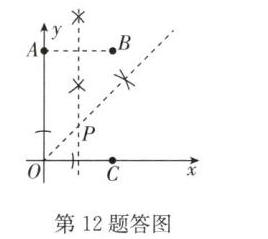
(2)∵$A(0,8)$,$B(4,8)$,
∴$AB// x$轴,
由作图知点P在线段AB的垂直平分线上,
∴点P的横坐标为2,
∵点P到$∠AOC$两边的距离相等,∴点P在第一象限的角平分线上,∴$P(2,2)$。
解:(1)如答图,点P为所作

(2)∵$A(0,8)$,$B(4,8)$,
∴$AB// x$轴,
由作图知点P在线段AB的垂直平分线上,
∴点P的横坐标为2,
∵点P到$∠AOC$两边的距离相等,∴点P在第一象限的角平分线上,∴$P(2,2)$。
13. (12分)如图,$A,B$为海中的两座小岛,$C$为海岸上的信号塔.已知小岛$A$在信号塔$C$的北偏西$54^{\circ}$方向80海里处,小岛$B$在信号塔$C$的南偏西$36^{\circ}$方向60海里处.
(1)求小岛$A$与小岛$B$之间的距离;
(2)一艘轮船从小岛$A$出发,沿直线向小岛$B$航行.若信号塔的信号有效覆盖半径为50海里,问:轮船在航行过程中,能否收到信号塔$C$的信号?

(1)求小岛$A$与小岛$B$之间的距离;
(2)一艘轮船从小岛$A$出发,沿直线向小岛$B$航行.若信号塔的信号有效覆盖半径为50海里,问:轮船在航行过程中,能否收到信号塔$C$的信号?

答案:
解:(1)如答图,由题意得$∠ACM = 54^{\circ}$,$∠BCN = 36^{\circ}$,
∴$∠ACB = 180^{\circ} - 54^{\circ} - 36^{\circ} = 90^{\circ}$。
∵$AC = 80$海里,$BC = 60$海里,
∴$AB = \sqrt{AC^{2} + BC^{2}} = 100$(海里),
∴小岛A与小岛B之间的距离是100海里。
(2)如答图,过点C作$CH⊥AB$于点H。
∵$△ABC$的面积$=\frac{1}{2}AB\cdot CH = \frac{1}{2}AC\cdot BC$,
∴$100CH = 60×80$,∴$CH = 48$。
∵信号塔的信号有效覆盖半径为50海里,
∴轮船在航行过程中,能收到信号塔C的信号。
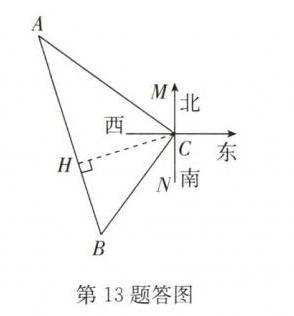
解:(1)如答图,由题意得$∠ACM = 54^{\circ}$,$∠BCN = 36^{\circ}$,
∴$∠ACB = 180^{\circ} - 54^{\circ} - 36^{\circ} = 90^{\circ}$。
∵$AC = 80$海里,$BC = 60$海里,
∴$AB = \sqrt{AC^{2} + BC^{2}} = 100$(海里),
∴小岛A与小岛B之间的距离是100海里。
(2)如答图,过点C作$CH⊥AB$于点H。
∵$△ABC$的面积$=\frac{1}{2}AB\cdot CH = \frac{1}{2}AC\cdot BC$,
∴$100CH = 60×80$,∴$CH = 48$。
∵信号塔的信号有效覆盖半径为50海里,
∴轮船在航行过程中,能收到信号塔C的信号。

14. (16分)如图,在平面直角坐标系$xOy$中,一次函数$y = 2x - 4$的图象与$x$轴、$y$轴分别交于点$A,B$,$P(m,n)(m > 0,n < 0)$为一次函数$y = 2x - 4$的图象上一点.
(1)求$A,B$两点的坐标;
(2)若$k = m + n$,求$k$的取值范围;
(3)若点$Q$为一次函数$y = 2x - 4$图象上第一象限内一点,且满足$OP = OQ,\angle POQ = 90^{\circ}$,求$m + n$的值;
(4)一次函数$y = - 3x + 1$的图象与一次函数$y = 2x - 4$的图象交于点$C$,与$y$轴交于点$D$,直线$OP$与直线$AB$、直线$CD$不能围成三角形,求出符合条件的点$P$的坐标.

(1)求$A,B$两点的坐标;
(2)若$k = m + n$,求$k$的取值范围;
(3)若点$Q$为一次函数$y = 2x - 4$图象上第一象限内一点,且满足$OP = OQ,\angle POQ = 90^{\circ}$,求$m + n$的值;
(4)一次函数$y = - 3x + 1$的图象与一次函数$y = 2x - 4$的图象交于点$C$,与$y$轴交于点$D$,直线$OP$与直线$AB$、直线$CD$不能围成三角形,求出符合条件的点$P$的坐标.

答案:
 解:(1)$y = 2x - 4$中,当$x = 0$时,$y = -4$,
解:(1)$y = 2x - 4$中,当$x = 0$时,$y = -4$,
则$B(0, -4)$,
当$y = 0$时,$2x - 4 = 0$,解得$x = 2$,则$A(2, 0)$。
(2)由题意知$n = 2m - 4 < 0$,则$m < 2$,
∵$k = m + n = m + 2m - 4 = 3m - 4$,且$0 < m < 2$,
∴$-4 < k < 2$。
(3)如答图①,过点P作$PM⊥y$轴于点M,过点Q作$QN⊥y$轴于点N,
则$∠PMO = ∠ONQ = 90^{\circ}$,
∴$∠POM + ∠OPM = 90^{\circ}$。
∵$∠POQ = 90^{\circ}$,
∴$∠POM + ∠QON = 90^{\circ}$,∴$∠OPM = ∠QON$。
又∵$OP = OQ$,∴$△POM≌△OQN(AAS)$,
由题意知,$P(m, 2m - 4)$,且$2m - 4 < 0$,
∴$PM = m$,$OM = 4 - 2m$,
∴$ON = PM = m$,$NQ = OM = 4 - 2m$,
∴点$Q(4 - 2m, m)$。
∵点Q在直线$y = 2x - 4$上,∴$2(4 - 2m) - 4 = m$,
解得$m = \frac{4}{5}$,∴$n = 2m - 4 = -\frac{12}{5}$,
则$m + n = \frac{4}{5} - \frac{12}{5} = -\frac{8}{5}$。
(4)设直线OP的函数表达式为$y = ax$,如答图②。
∵直线OP与直线AB、直线CD不能围成三角形,
∴直线$OP//$直线CD或直线OP过点C。
①若直线$OP//$直线CD,则$a = -3$,
∴直线OP的函数表达式为$y = -3x$,
由$\begin{cases}y = -3x\\y = 2x - 4\end{cases}$得$\begin{cases}x = \frac{4}{5}\\y = -\frac{12}{5}\end{cases}$,即$P(\frac{4}{5}, -\frac{12}{5})$;
②若直线OP过点C,
由$\begin{cases}y = 2x - 4\\y = -3x + 1\end{cases}$得$\begin{cases}x = 1\\y = -2\end{cases}$,
即点$C(1, -2)$,此时点$P(1, -2)$。
综上,符合条件的点P的坐标为$(\frac{4}{5}, -\frac{12}{5})$或$(1, -2)$。
 解:(1)$y = 2x - 4$中,当$x = 0$时,$y = -4$,
解:(1)$y = 2x - 4$中,当$x = 0$时,$y = -4$,则$B(0, -4)$,
当$y = 0$时,$2x - 4 = 0$,解得$x = 2$,则$A(2, 0)$。
(2)由题意知$n = 2m - 4 < 0$,则$m < 2$,
∵$k = m + n = m + 2m - 4 = 3m - 4$,且$0 < m < 2$,
∴$-4 < k < 2$。
(3)如答图①,过点P作$PM⊥y$轴于点M,过点Q作$QN⊥y$轴于点N,
则$∠PMO = ∠ONQ = 90^{\circ}$,
∴$∠POM + ∠OPM = 90^{\circ}$。
∵$∠POQ = 90^{\circ}$,
∴$∠POM + ∠QON = 90^{\circ}$,∴$∠OPM = ∠QON$。
又∵$OP = OQ$,∴$△POM≌△OQN(AAS)$,
由题意知,$P(m, 2m - 4)$,且$2m - 4 < 0$,
∴$PM = m$,$OM = 4 - 2m$,
∴$ON = PM = m$,$NQ = OM = 4 - 2m$,
∴点$Q(4 - 2m, m)$。
∵点Q在直线$y = 2x - 4$上,∴$2(4 - 2m) - 4 = m$,
解得$m = \frac{4}{5}$,∴$n = 2m - 4 = -\frac{12}{5}$,
则$m + n = \frac{4}{5} - \frac{12}{5} = -\frac{8}{5}$。
(4)设直线OP的函数表达式为$y = ax$,如答图②。
∵直线OP与直线AB、直线CD不能围成三角形,
∴直线$OP//$直线CD或直线OP过点C。
①若直线$OP//$直线CD,则$a = -3$,
∴直线OP的函数表达式为$y = -3x$,
由$\begin{cases}y = -3x\\y = 2x - 4\end{cases}$得$\begin{cases}x = \frac{4}{5}\\y = -\frac{12}{5}\end{cases}$,即$P(\frac{4}{5}, -\frac{12}{5})$;
②若直线OP过点C,
由$\begin{cases}y = 2x - 4\\y = -3x + 1\end{cases}$得$\begin{cases}x = 1\\y = -2\end{cases}$,
即点$C(1, -2)$,此时点$P(1, -2)$。
综上,符合条件的点P的坐标为$(\frac{4}{5}, -\frac{12}{5})$或$(1, -2)$。