1. 如图，在长方形 $ABCD$ 中，$AB = 6$，$BC = 2$，直线 $l$ 是长方形 $ABCD$ 的一条对称轴，且分别与 $AD$，$BC$ 交于点 $E$，$F$，若直线 $l$ 上的动点 $P$ 使得 $\triangle PAB$ 和 $\triangle PBC$ 均为等腰三角形，则动点 $P$ 的个数为。

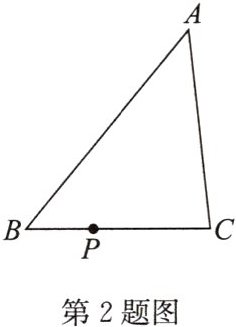
2. 如图，在 $\triangle ABC$ 中，$AB＞AC＞BC$，$P$ 为 $BC$ 上一点（不与点 $B$，$C$ 重合）。在 $AB$ 上找一点 $M$，在 $AC$ 上找一点 $N$，使得 $\triangle AMN$ 与 $\triangle PMN$ 全等，以下是甲、乙两位同学的作法。
甲：连接 $AP$，作线段 $AP$ 的垂直平分线，分别交 $AB$，$AC$ 于 $M$，$N$ 两点，则 $M$，$N$ 两点即为所求。
乙：过点 $P$ 作 $PM// AC$，交 $AB$ 于点 $M$，过点 $P$ 作 $PN// AB$，交 $AC$ 于点 $N$，则 $M$，$N$ 两点即为所求。
(1) 对于甲、乙两人的作法，下列判断正确的是（ ）
A. 两人都正确 B. 甲正确，乙错误 C. 甲错误，乙正确
(2) 选择一种你认为正确的作法，补全图形并证明。

3. 如图，在四边形 $ABCD$ 中，$\angle A=\angle B = 90^{\circ}$，$AB = 25\mathrm{cm}$，$DA = 15\mathrm{cm}$，$CB = 10\mathrm{cm}$。动点 $E$ 从 $A$ 点出发，以 $2\mathrm{cm/s}$ 的速度向 $B$ 点移动，设移动的时间为 $x\mathrm{s}$。
(1) 当 $x$ 为何值时，点 $E$ 在线段 $CD$ 的垂直平分线上？
(2) 在(1)的结论下，判断 $DE$ 与 $CE$ 的位置关系，并说明理由。