1. 已知 $\triangle ABC$ 是等边三角形,点 $D$ 在射线 $BC$ 上(不与点 $B$,$C$ 重合),点 $D$ 关于直线 $AC$ 的对称点为 $E$,连接 $AD$,$AE$,$CE$,$DE$。
(1) 如图①,当点 $D$ 为线段 $BC$ 的中点时,求证:$\triangle ADE$ 是等边三角形;
(2) 当点 $D$ 在线段 $BC$ 的延长线上时,先根据题意在图②中补全图形,再连接 $BE$,取线段 $BE$ 的中点记为 $F$,连接 $CF$。用等式表示线段 $AD$ 与 $CF$ 的数量关系,并证明。
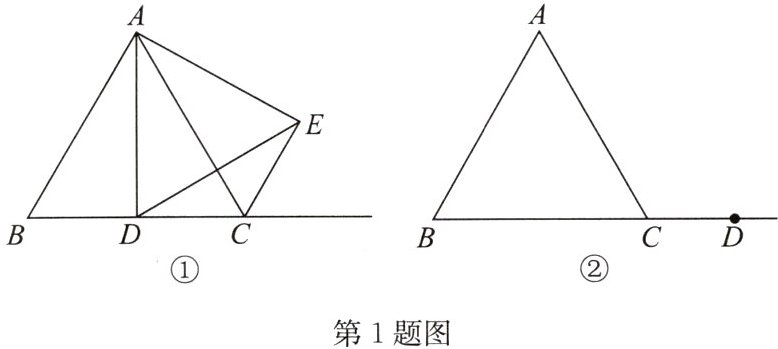
(1) 如图①,当点 $D$ 为线段 $BC$ 的中点时,求证:$\triangle ADE$ 是等边三角形;
(2) 当点 $D$ 在线段 $BC$ 的延长线上时,先根据题意在图②中补全图形,再连接 $BE$,取线段 $BE$ 的中点记为 $F$,连接 $CF$。用等式表示线段 $AD$ 与 $CF$ 的数量关系,并证明。

答案:
(1) 证明: ∵ 点 $ D $ 与点 $ E $ 关于直线 $ AC $ 对称,
$\therefore AD = AE$, $\angle DAC = \angle EAC$.
$\because \triangle ABC$ 是等边三角形, $\therefore AB = AC$, $\angle BAC = 60^{\circ}$.
$\because D$ 为线段 $ BC $ 的中点,
$\therefore \angle DAC = \frac{1}{2}\angle BAC = \frac{1}{2} \times 60^{\circ} = 30^{\circ}$,
$\therefore \angle DAC = \angle EAC = 30^{\circ}$, $\therefore \angle DAE = 60^{\circ}$.
$\because AD = AE$, $\therefore \triangle ADE$ 是等边三角形.
(2) 解: 补全图形如答图. 线段 $ AD $ 与 $ CF $ 的数量关系为 $ AD = 2CF $. 证明如下:
如答图, 延长 $ CF $ 到点 $ G $, 使 $ GF = CF $, 连接 $ BG $.

$\because F$ 为线段 $ BE $ 的中点, $\therefore BF = EF$.
在 $\triangle BFG$ 和 $\triangle EFC$ 中, $\left\{\begin{array}{l} GF = CF, \\ \angle BFG = \angle EFC, \\ BF = EF, \end{array}\right.$
$\therefore \triangle BFG \cong \triangle EFC$, $\therefore GB = CE$, $\angle G = \angle FCE$,
$\therefore BG // CE$.
$\because \triangle ABC$ 是等边三角形, $\therefore AC = BC$, $\angle ACB = 60^{\circ}$,
$\therefore \angle ACD = 120^{\circ}$.
$\because$ 点 $ D$, $ E $ 关于直线 $ AC $ 对称,
$\therefore CD = CE$, $\angle ACD = \angle ACE = 120^{\circ}$,
$\therefore CD = BG$, $\angle BCE = 60^{\circ}$.
$\because BG // CE$, $\therefore \angle BCE + \angle CBG = 180^{\circ}$, $\therefore \angle CBG = 120^{\circ}$.
$\therefore \angle ACD = \angle CBG$.
在 $\triangle ACD$ 和 $\triangle CBG$ 中, $\left\{\begin{array}{l} AC = CB, \\ \angle ACD = \angle CBG, \\ CD = BG, \end{array}\right.$
$\therefore \triangle ACD \cong \triangle CBG$, $\therefore AD = CG$, $\therefore AD = 2CF$.
(1) 证明: ∵ 点 $ D $ 与点 $ E $ 关于直线 $ AC $ 对称,
$\therefore AD = AE$, $\angle DAC = \angle EAC$.
$\because \triangle ABC$ 是等边三角形, $\therefore AB = AC$, $\angle BAC = 60^{\circ}$.
$\because D$ 为线段 $ BC $ 的中点,
$\therefore \angle DAC = \frac{1}{2}\angle BAC = \frac{1}{2} \times 60^{\circ} = 30^{\circ}$,
$\therefore \angle DAC = \angle EAC = 30^{\circ}$, $\therefore \angle DAE = 60^{\circ}$.
$\because AD = AE$, $\therefore \triangle ADE$ 是等边三角形.
(2) 解: 补全图形如答图. 线段 $ AD $ 与 $ CF $ 的数量关系为 $ AD = 2CF $. 证明如下:
如答图, 延长 $ CF $ 到点 $ G $, 使 $ GF = CF $, 连接 $ BG $.

$\because F$ 为线段 $ BE $ 的中点, $\therefore BF = EF$.
在 $\triangle BFG$ 和 $\triangle EFC$ 中, $\left\{\begin{array}{l} GF = CF, \\ \angle BFG = \angle EFC, \\ BF = EF, \end{array}\right.$
$\therefore \triangle BFG \cong \triangle EFC$, $\therefore GB = CE$, $\angle G = \angle FCE$,
$\therefore BG // CE$.
$\because \triangle ABC$ 是等边三角形, $\therefore AC = BC$, $\angle ACB = 60^{\circ}$,
$\therefore \angle ACD = 120^{\circ}$.
$\because$ 点 $ D$, $ E $ 关于直线 $ AC $ 对称,
$\therefore CD = CE$, $\angle ACD = \angle ACE = 120^{\circ}$,
$\therefore CD = BG$, $\angle BCE = 60^{\circ}$.
$\because BG // CE$, $\therefore \angle BCE + \angle CBG = 180^{\circ}$, $\therefore \angle CBG = 120^{\circ}$.
$\therefore \angle ACD = \angle CBG$.
在 $\triangle ACD$ 和 $\triangle CBG$ 中, $\left\{\begin{array}{l} AC = CB, \\ \angle ACD = \angle CBG, \\ CD = BG, \end{array}\right.$
$\therefore \triangle ACD \cong \triangle CBG$, $\therefore AD = CG$, $\therefore AD = 2CF$.
2. 在 $\triangle ABC$ 中,$\angle B = 60^{\circ}$,$D$ 是 $BC$ 上一点,且 $AD = AC$。
(1) 如图①,延长 $BC$ 到点 $E$,使 $CE = BD$,连接 $AE$。求证:$AB = AE$;
(2) 如图②,在 $AB$ 上取一点 $F$,使 $DF = DB$,$P$ 为 $BC$ 延长线上的点,连接 $PA$,$PF$。若 $PA = PF$,猜想 $PC$ 与 $BD$ 的数量关系并证明。

(1) 如图①,延长 $BC$ 到点 $E$,使 $CE = BD$,连接 $AE$。求证:$AB = AE$;
(2) 如图②,在 $AB$ 上取一点 $F$,使 $DF = DB$,$P$ 为 $BC$ 延长线上的点,连接 $PA$,$PF$。若 $PA = PF$,猜想 $PC$ 与 $BD$ 的数量关系并证明。

答案:
(1) 证明: 在 $\triangle ACD$ 中, $ AD = AC $, $\therefore \angle ADC = \angle ACD $,
$\therefore \angle ADB = \angle ACE$.
在 $\triangle ADB$ 和 $\triangle ACE$ 中, $\left\{\begin{array}{l} AD = AC, \\ \angle ADB = \angle ACE, \\ BD = CE, \end{array}\right.$
$\therefore \triangle ADB \cong \triangle ACE(SAS)$, $\therefore AB = AE$.
(2) 解: $ PC $ 与 $ BD $ 的数量关系为 $ PC = 2BD $.
证明: 在线段 $ PC $ 上取一点 $ E $, 使 $ CE = BD $, 连接 $ AE $, 如答图.

由 (1) 得 $\triangle ADB \cong \triangle ACE(SAS)$, $\therefore \angle AEC = \angle B = 60^{\circ}$,
$\therefore \angle AEP = 120^{\circ}$,
$\because DF = DB$, $\angle B = 60^{\circ}$, $\therefore \triangle DBF$ 是等边三角形,
$\therefore \angle FDB = \angle DFB = 60^{\circ}$,
$\therefore \angle PFD + \angle PFA = 120^{\circ}$, $\angle PDF = 120^{\circ}$,
$\therefore \angle AEP = \angle PDF$,
$\because PA = PF$, $\therefore \angle PAF = \angle PFA$,
$\because \angle APE + \angle PAF = 180^{\circ} - \angle B = 120^{\circ}$,
$\therefore \angle APE = \angle PFD$.
在 $\triangle APE$ 和 $\triangle PFD$ 中, $\left\{\begin{array}{l} \angle AEP = \angle PDF, \\ \angle APE = \angle PFD, \\ PA = PF, \end{array}\right.$
$\therefore \triangle APE \cong \triangle PFD(AAS)$, $\therefore PE = DF = BD = CE$,
$\therefore PC = 2BD$.
(1) 证明: 在 $\triangle ACD$ 中, $ AD = AC $, $\therefore \angle ADC = \angle ACD $,
$\therefore \angle ADB = \angle ACE$.
在 $\triangle ADB$ 和 $\triangle ACE$ 中, $\left\{\begin{array}{l} AD = AC, \\ \angle ADB = \angle ACE, \\ BD = CE, \end{array}\right.$
$\therefore \triangle ADB \cong \triangle ACE(SAS)$, $\therefore AB = AE$.
(2) 解: $ PC $ 与 $ BD $ 的数量关系为 $ PC = 2BD $.
证明: 在线段 $ PC $ 上取一点 $ E $, 使 $ CE = BD $, 连接 $ AE $, 如答图.

由 (1) 得 $\triangle ADB \cong \triangle ACE(SAS)$, $\therefore \angle AEC = \angle B = 60^{\circ}$,
$\therefore \angle AEP = 120^{\circ}$,
$\because DF = DB$, $\angle B = 60^{\circ}$, $\therefore \triangle DBF$ 是等边三角形,
$\therefore \angle FDB = \angle DFB = 60^{\circ}$,
$\therefore \angle PFD + \angle PFA = 120^{\circ}$, $\angle PDF = 120^{\circ}$,
$\therefore \angle AEP = \angle PDF$,
$\because PA = PF$, $\therefore \angle PAF = \angle PFA$,
$\because \angle APE + \angle PAF = 180^{\circ} - \angle B = 120^{\circ}$,
$\therefore \angle APE = \angle PFD$.
在 $\triangle APE$ 和 $\triangle PFD$ 中, $\left\{\begin{array}{l} \angle AEP = \angle PDF, \\ \angle APE = \angle PFD, \\ PA = PF, \end{array}\right.$
$\therefore \triangle APE \cong \triangle PFD(AAS)$, $\therefore PE = DF = BD = CE$,
$\therefore PC = 2BD$.