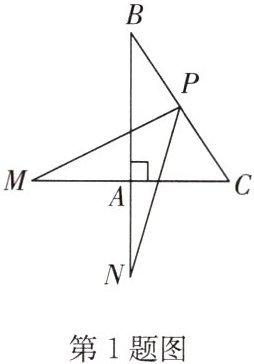
1. 如图,在△ABC 中,∠BAC = 90°,P 是 BC 的中点,M,N 分别是 CA,BA 延长线上的点,且 AM = AN = $\frac{1}{2}$BC,则∠MPN 的度数为______。

答案:
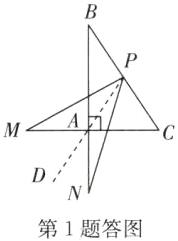
$45^{\circ}$ 点拨:如答图,连接 $PA$ 并延长到点 $D$.
$\because \angle BAC = 90^{\circ}$, $P$ 是 $BC$ 的中点,
$\therefore AP = \frac{1}{2}BC$, $\because AM = AN = \frac{1}{2}BC$, $\therefore AM = AP$, $AN = AP$, $\therefore \angle M = \angle APM$, $\angle N = \angle APN$,
$\because \angle DAM = \angle M + \angle APM$, $\angle DAN = \angle N + \angle APN$,
$\therefore \angle DAM = 2\angle APM$, $\angle DAN = 2\angle APN$,
$\therefore \angle MAN = \angle DAM + \angle DAN = 2\angle APM + 2\angle APN = 2(\angle APM + \angle APN) = 2\angle MPN$,
$\because \angle MAN = \angle BAC = 90^{\circ}$, $\therefore \angle MPN = \frac{1}{2}\angle MAN = 45^{\circ}$.
$45^{\circ}$ 点拨:如答图,连接 $PA$ 并延长到点 $D$.
$\because \angle BAC = 90^{\circ}$, $P$ 是 $BC$ 的中点,
$\therefore AP = \frac{1}{2}BC$, $\because AM = AN = \frac{1}{2}BC$, $\therefore AM = AP$, $AN = AP$, $\therefore \angle M = \angle APM$, $\angle N = \angle APN$,
$\because \angle DAM = \angle M + \angle APM$, $\angle DAN = \angle N + \angle APN$,
$\therefore \angle DAM = 2\angle APM$, $\angle DAN = 2\angle APN$,
$\therefore \angle MAN = \angle DAM + \angle DAN = 2\angle APM + 2\angle APN = 2(\angle APM + \angle APN) = 2\angle MPN$,
$\because \angle MAN = \angle BAC = 90^{\circ}$, $\therefore \angle MPN = \frac{1}{2}\angle MAN = 45^{\circ}$.

2. 如图①,在锐角三角形 ABC 中,CD,BE 分别是 AB,AC 边上的高,M,N 分别是线段 BC,DE 的中点,连接 DM,ME,MN。
(1) 求证:MN⊥DE。
(2) 猜想∠BAC 与∠DME 之间的关系,并证明你的猜想。
(3) 当∠BAC 变为钝角时,如图②,上述(1)(2)中的结论是否还成立?若成立,直接回答,不需证明;若不成立,请说明理由。

(1) 求证:MN⊥DE。
(2) 猜想∠BAC 与∠DME 之间的关系,并证明你的猜想。
(3) 当∠BAC 变为钝角时,如图②,上述(1)(2)中的结论是否还成立?若成立,直接回答,不需证明;若不成立,请说明理由。

答案:(1) 证明: $\because CD$, $BE$ 分别是 $AB$, $AC$ 边上的高, $M$ 是 $BC$ 的中点,
$\therefore DM = \frac{1}{2}BC$, $ME = \frac{1}{2}BC$, $\therefore DM = ME$.
$\because N$ 为 $DE$ 的中点, $\therefore MN \perp DE$.
(2) 解: $\angle DME = 180^{\circ} - 2\angle BAC$. 证明如下:
在 $\triangle ABC$ 中, $\angle ABC + \angle ACB = 180^{\circ} - \angle BAC$,
$\because DM = ME = BM = MC$,
$\therefore \angle BMD + \angle CME = (180^{\circ} - 2\angle ABC) + (180^{\circ} - 2\angle ACB) = 360^{\circ} - 2(\angle ABC + \angle ACB) = 360^{\circ} - 2(180^{\circ} - \angle BAC) = 2\angle BAC$,
$\therefore \angle DME = 180^{\circ} - 2\angle BAC$.
(3) 解: (1) 中结论成立, (2) 中结论不成立. 理由如下:
在 $\triangle ABC$ 中, $\angle ABC + \angle ACB = 180^{\circ} - \angle BAC$,
$\because DM = ME = BM = MC$,
$\therefore \angle BME + \angle CMD = 2\angle ACB + 2\angle ABC = 2(180^{\circ} - \angle BAC) = 360^{\circ} - 2\angle BAC$,
$\therefore \angle DME = 180^{\circ} - (360^{\circ} - 2\angle BAC) = 2\angle BAC - 180^{\circ}$.
$\therefore DM = \frac{1}{2}BC$, $ME = \frac{1}{2}BC$, $\therefore DM = ME$.
$\because N$ 为 $DE$ 的中点, $\therefore MN \perp DE$.
(2) 解: $\angle DME = 180^{\circ} - 2\angle BAC$. 证明如下:
在 $\triangle ABC$ 中, $\angle ABC + \angle ACB = 180^{\circ} - \angle BAC$,
$\because DM = ME = BM = MC$,
$\therefore \angle BMD + \angle CME = (180^{\circ} - 2\angle ABC) + (180^{\circ} - 2\angle ACB) = 360^{\circ} - 2(\angle ABC + \angle ACB) = 360^{\circ} - 2(180^{\circ} - \angle BAC) = 2\angle BAC$,
$\therefore \angle DME = 180^{\circ} - 2\angle BAC$.
(3) 解: (1) 中结论成立, (2) 中结论不成立. 理由如下:
在 $\triangle ABC$ 中, $\angle ABC + \angle ACB = 180^{\circ} - \angle BAC$,
$\because DM = ME = BM = MC$,
$\therefore \angle BME + \angle CMD = 2\angle ACB + 2\angle ABC = 2(180^{\circ} - \angle BAC) = 360^{\circ} - 2\angle BAC$,
$\therefore \angle DME = 180^{\circ} - (360^{\circ} - 2\angle BAC) = 2\angle BAC - 180^{\circ}$.