1. 从三角形的一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,若分得的两个小三角形中一个三角形为等腰三角形,另一个三角形的三个内角与原来三角形的三个内角分别相等,则称这条线段为这个三角形的“等角分割线”。例如,等腰直角三角形斜边上的高就是这个等腰直角三角形的一条“等角分割线”。
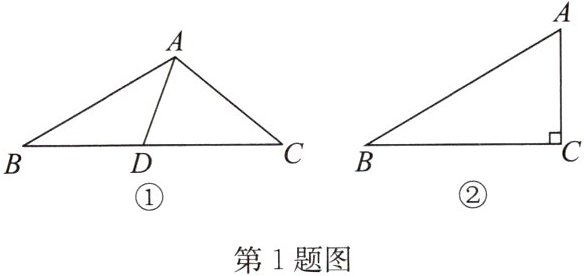
(1)如图①,在$\triangle ABC$中,$D$是边$BC$上一点,若$\angle B = 30^{\circ}$,$\angle BAD = \angle C = 40^{\circ}$,求证:$AD$为$\triangle ABC$的“等角分割线”。
(2)如图②,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$。
①利用直尺和圆规,作出$\triangle ABC$的“等角分割线”;
②若$BC = 6$,求①中画出的“等角分割线”的长度。
(3)在$\triangle ABC$中,$\angle A = 42^{\circ}$,若$\triangle ABC$存在“等角分割线”$CD$,求出所有符合要求的$\angle ACB$的度数。
(1)如图①,在$\triangle ABC$中,$D$是边$BC$上一点,若$\angle B = 30^{\circ}$,$\angle BAD = \angle C = 40^{\circ}$,求证:$AD$为$\triangle ABC$的“等角分割线”。
(2)如图②,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$。
①利用直尺和圆规,作出$\triangle ABC$的“等角分割线”;
②若$BC = 6$,求①中画出的“等角分割线”的长度。
(3)在$\triangle ABC$中,$\angle A = 42^{\circ}$,若$\triangle ABC$存在“等角分割线”$CD$,求出所有符合要求的$\angle ACB$的度数。

答案:
1.(1)证明:∵∠B = 30°,∠BAD = ∠C = 40°,
∴∠ADB = ∠BAC = 180°−40°−30° = 110°.
又∵∠B = ∠B,
∴△ABD的三个内角与△ABC的三个内角的度数分别相等.
∵∠B = 30°,∠BAD = 40°,
∴∠ADC = ∠B + ∠BAD = 70°.
又∵∠BAC = 110°,
∴∠DAC = ∠BAC - ∠BAD = 70° = ∠ADC,
∴AC = DC,∴△ACD是等腰三角形,
∴AD为△ABC的“等角分割线”.
(2)解:①如答图,作∠BAC的平分线,交BC于点D,线段AD即为所求.理由如下:
∵∠C = 90°,∠B = 30°,∴∠BAC = 90°−30° = 60°.
∵AD平分∠BAC,∴∠DAC = ∠DAB = 30° = ∠B,
∴∠ADC = 60° = ∠BAC;
又∵∠C = ∠C,
∴△ADC的三个内角与△ABC的三个内角分别相等.∵∠BAD = ∠B,∴AD = BD,∴△ABD是等腰三角形,∴AD为△ABC的“等角分割线”.
②设CD = x.
∵在△ADC中,∠C = 90°,∠DAC = 30°,
∴AD = 2CD = 2x,∴BD = AD = 2x.
∵BC = 6,∴x + 2x = 6,∴x = 2,∴AD = 2x = 4.

(3)解:当△ACD是等腰三角形,DA = DC时,∠ACD = ∠A = 42°,∴∠ACB = ∠BDC = 42° + 42° = 84°;
当△ACD是等腰三角形,DA = AC时,∠ACD = ∠ADC = 69°,∠BCD = ∠A = 42°,
∴∠ACB = 69° + 42° = 111°;
当△ACD是等腰三角形,CD = AC时,不存在;
当△BCD是等腰三角形,DC = BD时,∠ACD = ∠BCD = ∠B = 46°,∴∠ACB = 92°;
当△BCD是等腰三角形,DB = BC时,∠BDC = ∠BCD,设∠BDC = ∠BCD = x,则∠B = 180°−2x,
则∠ACD = ∠B = 180°−2x,
由题意得,180°−2x + 42° = x,解得x = 74°,
∴∠ACD = 180°−2x = 32°,∴∠ACB = 106°;
当△BCD是等腰三角形,CD = CB时,不存在.
综上,∠ACB的度数为84°或111°或92°或106°.
1.(1)证明:∵∠B = 30°,∠BAD = ∠C = 40°,
∴∠ADB = ∠BAC = 180°−40°−30° = 110°.
又∵∠B = ∠B,
∴△ABD的三个内角与△ABC的三个内角的度数分别相等.
∵∠B = 30°,∠BAD = 40°,
∴∠ADC = ∠B + ∠BAD = 70°.
又∵∠BAC = 110°,
∴∠DAC = ∠BAC - ∠BAD = 70° = ∠ADC,
∴AC = DC,∴△ACD是等腰三角形,
∴AD为△ABC的“等角分割线”.
(2)解:①如答图,作∠BAC的平分线,交BC于点D,线段AD即为所求.理由如下:
∵∠C = 90°,∠B = 30°,∴∠BAC = 90°−30° = 60°.
∵AD平分∠BAC,∴∠DAC = ∠DAB = 30° = ∠B,
∴∠ADC = 60° = ∠BAC;
又∵∠C = ∠C,
∴△ADC的三个内角与△ABC的三个内角分别相等.∵∠BAD = ∠B,∴AD = BD,∴△ABD是等腰三角形,∴AD为△ABC的“等角分割线”.
②设CD = x.
∵在△ADC中,∠C = 90°,∠DAC = 30°,
∴AD = 2CD = 2x,∴BD = AD = 2x.
∵BC = 6,∴x + 2x = 6,∴x = 2,∴AD = 2x = 4.

(3)解:当△ACD是等腰三角形,DA = DC时,∠ACD = ∠A = 42°,∴∠ACB = ∠BDC = 42° + 42° = 84°;
当△ACD是等腰三角形,DA = AC时,∠ACD = ∠ADC = 69°,∠BCD = ∠A = 42°,
∴∠ACB = 69° + 42° = 111°;
当△ACD是等腰三角形,CD = AC时,不存在;
当△BCD是等腰三角形,DC = BD时,∠ACD = ∠BCD = ∠B = 46°,∴∠ACB = 92°;
当△BCD是等腰三角形,DB = BC时,∠BDC = ∠BCD,设∠BDC = ∠BCD = x,则∠B = 180°−2x,
则∠ACD = ∠B = 180°−2x,
由题意得,180°−2x + 42° = x,解得x = 74°,
∴∠ACD = 180°−2x = 32°,∴∠ACB = 106°;
当△BCD是等腰三角形,CD = CB时,不存在.
综上,∠ACB的度数为84°或111°或92°或106°.