1. 对于实数 $ a,b $,定义 $ \min\{ a,b\} $ 为:当 $ a\leqslant b $ 时, $ \min\{ a,b\} =a $;当 $ a>b $ 时, $ \min\{ a,b\} =b $。例如: $ \min\{ 1,-2\} =-2 $。已知 $ \min\{ \sqrt {30},a\} =a $, $ \min\{ \sqrt {30},b\} =\sqrt {30} $,且 $ a $ 和 $ b $ 为两个连续正整数,则 $ 2a - b $ 的值为(
A. 1
B. 2
C. 3
D. 4
D
)A. 1
B. 2
C. 3
D. 4
答案:D 点拨:$\because \min\{\sqrt{30},a\}=a,\min\{\sqrt{30},b\}=\sqrt{30},\therefore a\leqslant \sqrt{30},b\geqslant \sqrt{30}.\because a,b$是两个连续的正整数,$\therefore a=5,b=6.\therefore 2a-b=2\times 5-6=4$. 故选 D.
2. $ a_{1}=1+\frac {1}{1^{2}}+\frac {1}{2^{2}} $, $ a_{2}=1+\frac {1}{2^{2}}+\frac {1}{3^{2}} $, $ a_{3}=1+\frac {1}{3^{2}}+\frac {1}{4^{2}} $, $ \cdots $, $ a_{n}=1+\frac {1}{n^{2}}+\frac {1}{(n+1)^{2}} $,其中 $ n $ 为正整数,则 $ \sqrt {a_{1}}+\sqrt {a_{2}}+\sqrt {a_{3}}+\cdots +\sqrt {a_{2025}} $ 的值是______。
$2025\frac{2025}{2026}$
答案:$2025\frac{2025}{2026}$ 点拨:$\because a_1=1+\frac{1}{1^2}+\frac{1}{2^2}=(\frac{3}{2})^2,a_2=1+\frac{1}{2^2}+\frac{1}{3^2}=(\frac{7}{6})^2,a_3=1+\frac{1}{3^2}+\frac{1}{4^2}=(\frac{13}{12})^2,\cdots,a_n=1+\frac{1}{n^2}+\frac{1}{(n+1)^2}=[\frac{n(n+1)+1}{n(n+1)}]^2,\therefore \sqrt{a_1}+\sqrt{a_2}+\sqrt{a_3}+\cdots+\sqrt{a_{2025}}=\frac{3}{2}+\frac{7}{6}+\frac{13}{12}+\cdots+\frac{2025\times 2026+1}{2025\times 2026}=1+\frac{1}{2}+1+\frac{1}{6}+1+\frac{1}{12}+\cdots+1+\frac{1}{2025\times 2026}=2025+(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{2025}-\frac{1}{2026})=2025+1-\frac{1}{2026}=2025\frac{2025}{2026}$.
3. 如图,等腰 $ \text{Rt}\triangle ABC $ 的斜边为 $ AB $, $ AB = AD $, $ CD// AB $(点 $ D $ 在点 $ C $ 左侧),连接 $ BD $,则 $ \frac {BD}{CD} $ 的值为______。
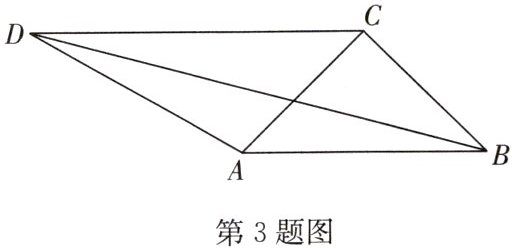

答案:$\sqrt{2}$
4. 已知 $ \sqrt {x + 2} + |y - 3| = 0 $,且 $ \sqrt [3]{2 - 3z} $ 与 $ \sqrt [3]{4z - 3} $ 互为相反数,求 $ yz - x $ 的平方根。
$\pm \sqrt{5}$
答案:解:因为$\sqrt{x+2}+|y-3|=0$,
所以$x+2=0,y-3=0$,所以$x=-2,y=3$.
因为$\sqrt[3]{2-3z}$与$\sqrt[3]{4z-3}$互为相反数,
所以$2-3z+4z-3=0$,所以$z=1$,
所以$yz-x=3× 1-(-2)=5$.
因为 5 的平方根是$\pm \sqrt{5}$,所以$yz-x$的平方根为$\pm \sqrt{5}$.
所以$x+2=0,y-3=0$,所以$x=-2,y=3$.
因为$\sqrt[3]{2-3z}$与$\sqrt[3]{4z-3}$互为相反数,
所以$2-3z+4z-3=0$,所以$z=1$,
所以$yz-x=3× 1-(-2)=5$.
因为 5 的平方根是$\pm \sqrt{5}$,所以$yz-x$的平方根为$\pm \sqrt{5}$.