1. 两条直线 $ y = k_1x + b_1 $ 和 $ y = k_2x + b_2 $ 相交于点 $ A(-2,3) $,则方程组 $ \begin{cases} k_1x - y + b_1 = 0, \\ k_2x - y + b_2 = 0 \end{cases} $ 的解是(
A. $ \begin{cases} x = 2 \\ y = 3 \end{cases} $
B. $ \begin{cases} x = 3 \\ y = 2 \end{cases} $
C. $ \begin{cases} x = -2 \\ y = 3 \end{cases} $
D. $ \begin{cases} x = 3 \\ y = -2 \end{cases} $
C
)A. $ \begin{cases} x = 2 \\ y = 3 \end{cases} $
B. $ \begin{cases} x = 3 \\ y = 2 \end{cases} $
C. $ \begin{cases} x = -2 \\ y = 3 \end{cases} $
D. $ \begin{cases} x = 3 \\ y = -2 \end{cases} $
答案:C
2. 如图,一次函数 $ y = kx + b $ 和 $ y = -\frac{1}{3}x + \frac{1}{3} $ 的图象交于点 $ M $,则关于 $ x $,$ y $ 的二元一次方程组 $ \begin{cases} y = kx + b, \\ y = -\frac{1}{3}x + \frac{1}{3} \end{cases} $ 的解是
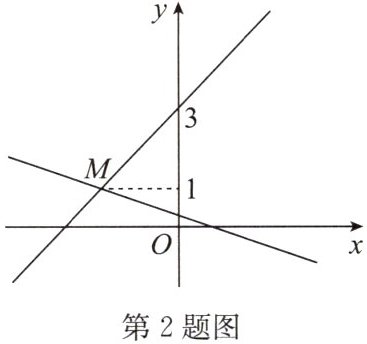
$\left\{\begin{array}{l} x=-2\\ y=1\end{array}\right. $
。
答案:$\left\{\begin{array}{l} x=-2\\ y=1\end{array}\right. $ 点拨:把$y=1$代入$y=-\frac {1}{3}x+\frac {1}{3}$得$-\frac {1}{3}x+\frac {1}{3}=1$,解得$x=-2$,所以点 M 的坐标为$(-2,1)$,所以关于x,y 的二元一次方程组$\left\{\begin{array}{l} y=kx+b,\\ y=-\frac {1}{3}x+\frac {1}{3}\end{array}\right. $的解是$\left\{\begin{array}{l} x=-2,\\ y=1.\end{array}\right. $
3. 一般地,二元一次方程的解可以转化为点的坐标,其中 $ x $ 的值对应的点的横坐标,$ y $ 的值对应为点的纵坐标,如二元一次方程 $ x - 2y = 0 $ 的解 $ \begin{cases} x = 0, \\ y = 0 \end{cases} $ 和 $ \begin{cases} x = 2, \\ y = 1 \end{cases} $ 可以分别转化为点 $ A(0,0) $ 和 $ B(2,1) $。以方程 $ x - 2y = 0 $ 的解为坐标的点的全体叫作方程 $ x - 2y = 0 $ 的图象。
(1) 写出二元一次方程 $ x - 2y = 0 $ 的任意一组解:______,并把它转化为点 $ C $ 的坐标:______;
(2) 在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,如方程 $ x - 2y = 0 $ 的图象由该方程所有的解转化成的点组成,在图中描出点 $ A $、点 $ B $ 和点 $ C $,观察它们是否在同一直线上;
(3) 取满足二元一次方程 $ x + y = 3 $ 的两个解,并把它们转化成点的坐标,画出二元一次方程 $ x + y = 3 $ 的图象;
(4) 根据图象,得出二元一次方程 $ x - 2y = 0 $ 的图象和二元一次方程 $ x + y = 3 $ 的图象的交点坐标为______,由此可得二元一次方程组 $ \begin{cases} x - 2y = 0, \\ x + y = 3 \end{cases} $ 的解是______。

(1) 写出二元一次方程 $ x - 2y = 0 $ 的任意一组解:______,并把它转化为点 $ C $ 的坐标:______;
(2) 在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,如方程 $ x - 2y = 0 $ 的图象由该方程所有的解转化成的点组成,在图中描出点 $ A $、点 $ B $ 和点 $ C $,观察它们是否在同一直线上;
(3) 取满足二元一次方程 $ x + y = 3 $ 的两个解,并把它们转化成点的坐标,画出二元一次方程 $ x + y = 3 $ 的图象;
(4) 根据图象,得出二元一次方程 $ x - 2y = 0 $ 的图象和二元一次方程 $ x + y = 3 $ 的图象的交点坐标为______,由此可得二元一次方程组 $ \begin{cases} x - 2y = 0, \\ x + y = 3 \end{cases} $ 的解是______。

答案:
(1)$\left\{\begin{array}{l} x=-2\\ y=-1\end{array}\right. $ $(-2,-1)$(答案不唯一)
(2)解:如答图,点 A、点 B 和点 C 在同一直线上.

(3)解:二元一次方程$x+y=3$的两个解为$\left\{\begin{array}{l} x=3,\\ y=0\end{array}\right. $或$\left\{\begin{array}{l} x=0,\\ y=3,\end{array}\right. $把它们转化成点的坐标为$(3,0),(0,3)$,如答图.(答案不唯一)
(4)$(2,1)$ $\left\{\begin{array}{l} x=2\\ y=1\end{array}\right. $
(1)$\left\{\begin{array}{l} x=-2\\ y=-1\end{array}\right. $ $(-2,-1)$(答案不唯一)
(2)解:如答图,点 A、点 B 和点 C 在同一直线上.

(3)解:二元一次方程$x+y=3$的两个解为$\left\{\begin{array}{l} x=3,\\ y=0\end{array}\right. $或$\left\{\begin{array}{l} x=0,\\ y=3,\end{array}\right. $把它们转化成点的坐标为$(3,0),(0,3)$,如答图.(答案不唯一)
(4)$(2,1)$ $\left\{\begin{array}{l} x=2\\ y=1\end{array}\right. $