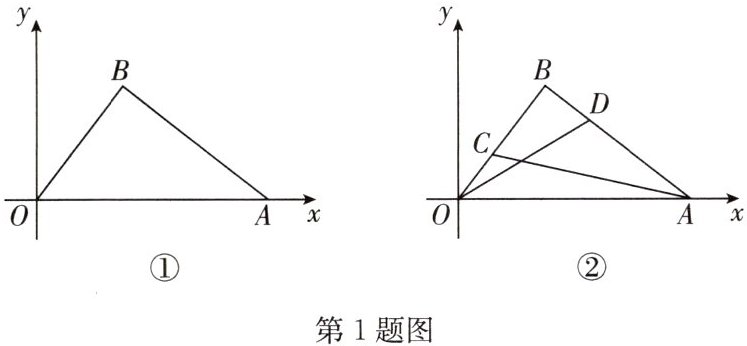
1. 如图①,在平面直角坐标系中,点 A 的坐标为$(5,0)$,点 B 在第一象限内,且$AB = 4$,$OB = 3$。
(1)试判断$\triangle AOB$的形状,并说明理由;
(2)点 P 是线段 OA 上一点,且$PB - PA = 1$,求点 P 的坐标;
(3)如图②,点 C,D 分别为线段 OB,BA 上的动点,且$OC = BD$,求$AC + OD$的最小值。
(1)试判断$\triangle AOB$的形状,并说明理由;
(2)点 P 是线段 OA 上一点,且$PB - PA = 1$,求点 P 的坐标;
(3)如图②,点 C,D 分别为线段 OB,BA 上的动点,且$OC = BD$,求$AC + OD$的最小值。

答案:
解:(1)△AOB是以OA为斜边的直角三角形.理由如下:∵A(5,0),∴OA=5,
∴AB²+OB²=4²+3²=25=5²=OA²,
∴△AOB是以OA为斜边的直角三角形.
(2)如答图①,过点B作BE⊥OA于点E,则$\frac{1}{2}$×OA×BE=$\frac{1}{2}$×OB×AB,即$\frac{1}{2}$×5×BE=$\frac{1}{2}$×3×4,∴BE=$\frac{12}{5}$,∴AE=$\frac{16}{5}$.设PA=m,则PB=m+1,由BE²+PE²=BP²,得($\frac{12}{5}$)²+($\frac{16}{5}$−m)²=(m+1)²,解得m=$\frac{25}{14}$,∴P($\frac{45}{14}$,0).


(3)如答图②,过点O作以OB为腰,∠BOH=90°的等腰直角三角形,∴HO=BO,∠HOC=∠OBD=90°,
∵OC=DB,∴△HOC≌△OBD(SAS),
∴OD=HC,∴AC+OD=AC+HC,
∴要使AC+OD最小,则AC+CH最小,
∴当A,C,H三点共线时,AC+CH最小,
即AC+OD的最小值为AH的长,
可求得B($\frac{9}{5}$,$\frac{12}{5}$),∴H(−$\frac{12}{5}$,$\frac{9}{5}$),
∴AH=$\sqrt{(-\frac{12}{5}-5)^{2}+(\frac{9}{5})^{2}}=\sqrt{58}$
即AC+OD的最小值为$\sqrt{58}$
解:(1)△AOB是以OA为斜边的直角三角形.理由如下:∵A(5,0),∴OA=5,
∴AB²+OB²=4²+3²=25=5²=OA²,
∴△AOB是以OA为斜边的直角三角形.
(2)如答图①,过点B作BE⊥OA于点E,则$\frac{1}{2}$×OA×BE=$\frac{1}{2}$×OB×AB,即$\frac{1}{2}$×5×BE=$\frac{1}{2}$×3×4,∴BE=$\frac{12}{5}$,∴AE=$\frac{16}{5}$.设PA=m,则PB=m+1,由BE²+PE²=BP²,得($\frac{12}{5}$)²+($\frac{16}{5}$−m)²=(m+1)²,解得m=$\frac{25}{14}$,∴P($\frac{45}{14}$,0).


(3)如答图②,过点O作以OB为腰,∠BOH=90°的等腰直角三角形,∴HO=BO,∠HOC=∠OBD=90°,
∵OC=DB,∴△HOC≌△OBD(SAS),
∴OD=HC,∴AC+OD=AC+HC,
∴要使AC+OD最小,则AC+CH最小,
∴当A,C,H三点共线时,AC+CH最小,
即AC+OD的最小值为AH的长,
可求得B($\frac{9}{5}$,$\frac{12}{5}$),∴H(−$\frac{12}{5}$,$\frac{9}{5}$),
∴AH=$\sqrt{(-\frac{12}{5}-5)^{2}+(\frac{9}{5})^{2}}=\sqrt{58}$
即AC+OD的最小值为$\sqrt{58}$