1.[综合实践]在学习全等三角形的知识时,数学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成的,在相对位置变化的同时,始终存在一对全等三角形.兴趣小组成员经过研讨给出定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,可以形象地看作两双手,所以通常称为“手拉手模型”.如图①,△ABC与△ADE都是等腰三角形,其中∠BAC=∠DAE,则△ABD≌△ACE(SAS).
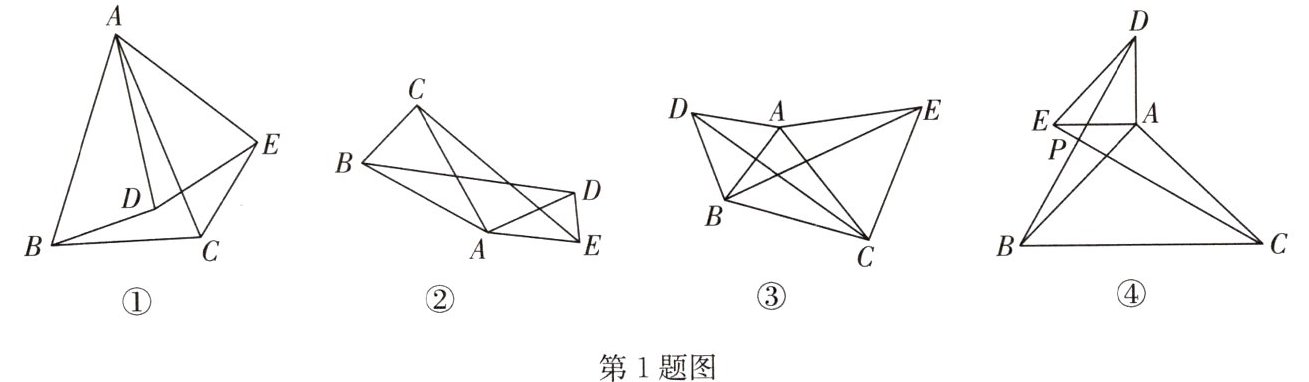
[初步把握]如图②,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,则有
[深入研究]如图③,已知△ABC,以AB,AC为边分别向外作等边△ABD和等边△ACE,并连接BE,CD,求证:BE=CD;
[拓展延伸]如图④,在△ABC和△ADE中,AB=AC,AE=AD,∠BAC=∠DAE=90°,连接BD,CE交于点P,请判断BD和CE的关系,并说明理由.

[初步把握]如图②,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,则有
△ABD
≌△ACE
;[深入研究]如图③,已知△ABC,以AB,AC为边分别向外作等边△ABD和等边△ACE,并连接BE,CD,求证:BE=CD;
[深入研究]证明:∵△ABD和△ACE都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,{AB=AD,∠BAE=∠DAC,AE=AC,
∴△ABE≌△ADC(SAS),
∴BE=CD.
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,{AB=AD,∠BAE=∠DAC,AE=AC,
∴△ABE≌△ADC(SAS),
∴BE=CD.
[拓展延伸]如图④,在△ABC和△ADE中,AB=AC,AE=AD,∠BAC=∠DAE=90°,连接BD,CE交于点P,请判断BD和CE的关系,并说明理由.
[拓展延伸]解:BD=CE,BD⊥CE.理由:
∵∠BAC=∠DAE=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠BAD,在△ABD和△ACE中,
{AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE.
∵∠BPC+∠ABD=∠BAC+∠ACE,
∴∠BPC=∠BAC=90°,∴BD⊥CE.
∵∠BAC=∠DAE=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠BAD,在△ABD和△ACE中,
{AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE.
∵∠BPC+∠ABD=∠BAC+∠ACE,
∴∠BPC=∠BAC=90°,∴BD⊥CE.
答案:1.[初步把握]△ABD △ACE
[深入研究]证明:∵△ABD和△ACE都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,{AB=AD,∠BAE=∠DAC,AE=AC,
∴△ABE≌△ADC(SAS),
∴BE=CD.
[拓展延伸]解:BD=CE,BD⊥CE.理由:
∵∠BAC=∠DAE=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠BAD,在△ABD和△ACE中,
{AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE.
∵∠BPC+∠ABD=∠BAC+∠ACE,
∴∠BPC=∠BAC=90°,∴BD⊥CE.
[深入研究]证明:∵△ABD和△ACE都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,{AB=AD,∠BAE=∠DAC,AE=AC,
∴△ABE≌△ADC(SAS),
∴BE=CD.
[拓展延伸]解:BD=CE,BD⊥CE.理由:
∵∠BAC=∠DAE=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠BAD,在△ABD和△ACE中,
{AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE.
∵∠BPC+∠ABD=∠BAC+∠ACE,
∴∠BPC=∠BAC=90°,∴BD⊥CE.