1. 平面直角坐标系中有一点$P(2a - 4,a + 3)$,请根据题意回答下列问题:
(1) 若点$P$在$x$轴上,求点$P$的坐标;
(2) 若点$Q$的坐标为$(6,-1)$,且$PQ// y$轴,求点$P$的坐标;
(3) 若点$P$到$y$轴的距离为$2$,求$a$的值。
(1) 若点$P$在$x$轴上,求点$P$的坐标;
(2) 若点$Q$的坐标为$(6,-1)$,且$PQ// y$轴,求点$P$的坐标;
(3) 若点$P$到$y$轴的距离为$2$,求$a$的值。
答案:解:(1)∵点P(2a−4,a+3)在x轴上,
∴a+3=0,解得a=−3,
∴2a−4=2×(−3)−4=−10,
∴点P的坐标为(−10,0).
(2)∵PQ//y轴,∴2a−4=6,解得a=5,
∴a+3=5+3=8,∴点P的坐标为(6,8).
(3)∵点P到y轴的距离为2,∴|2a−4|=2,
∴2a−4=2或2a−4=−2,解得a=3或a=1.
故a的值为3或1.
∴a+3=0,解得a=−3,
∴2a−4=2×(−3)−4=−10,
∴点P的坐标为(−10,0).
(2)∵PQ//y轴,∴2a−4=6,解得a=5,
∴a+3=5+3=8,∴点P的坐标为(6,8).
(3)∵点P到y轴的距离为2,∴|2a−4|=2,
∴2a−4=2或2a−4=−2,解得a=3或a=1.
故a的值为3或1.
2. 已知,$A(0,1)$,$B(2,0)$,$C(4,3)$。
(1) 如图,在坐标系中描出各点,画出$\triangle ABC$;
(2) 求$\triangle ABC$的面积;
(3) 设点$P$在坐标轴上,且$\triangle ABP$与$\triangle ABC$的面积相等,求点$P$的坐标。
(1) 如图,在坐标系中描出各点,画出$\triangle ABC$;
(2) 求$\triangle ABC$的面积;
(3) 设点$P$在坐标轴上,且$\triangle ABP$与$\triangle ABC$的面积相等,求点$P$的坐标。

答案:
解:(1)如答图.
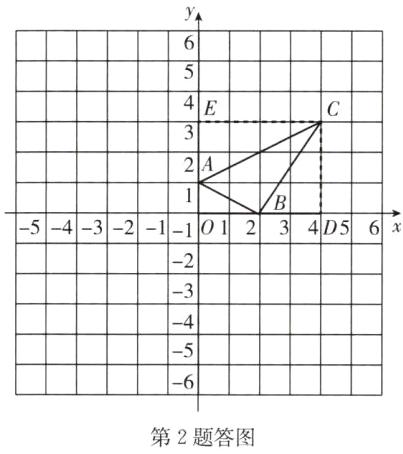
(2)如答图,过点C向x轴,y轴作垂线,垂足分别为D,E;∴四边形DOEC的面积=3×4=12,△BCD的面积=
$\frac{1}{2}$×2×3=3,△ACE的面积=$\frac{1}{2}$×2×4=4,△AOB的面积=$\frac{1}{2}$×2×1=1.∴△ABC的面积=四边形DOEC的面积−△ACE的面积−△BCD的面积−△AOB的面积=12 −4−3−1=4.
(3)当点P在x轴上时,△ABP的面积=$\frac{1}{2}$BP·AO=4,即$\frac{1}{2}$×BP×1=4,解得BP=8,
∴点P的坐标为(10,0)或(−6,0);
当点P在y轴上时,△ABP的面积=$\frac{1}{2}$×AP×BO=4,即$\frac{1}{2}$×AP×2=4,解得AP=4,
∴点P的坐标为(0,5)或(0,−3).
综上可知,点P的坐标为(0,5)或(0,−3)或(10,0)或(−6,0).
解:(1)如答图.

(2)如答图,过点C向x轴,y轴作垂线,垂足分别为D,E;∴四边形DOEC的面积=3×4=12,△BCD的面积=
$\frac{1}{2}$×2×3=3,△ACE的面积=$\frac{1}{2}$×2×4=4,△AOB的面积=$\frac{1}{2}$×2×1=1.∴△ABC的面积=四边形DOEC的面积−△ACE的面积−△BCD的面积−△AOB的面积=12 −4−3−1=4.
(3)当点P在x轴上时,△ABP的面积=$\frac{1}{2}$BP·AO=4,即$\frac{1}{2}$×BP×1=4,解得BP=8,
∴点P的坐标为(10,0)或(−6,0);
当点P在y轴上时,△ABP的面积=$\frac{1}{2}$×AP×BO=4,即$\frac{1}{2}$×AP×2=4,解得AP=4,
∴点P的坐标为(0,5)或(0,−3).
综上可知,点P的坐标为(0,5)或(0,−3)或(10,0)或(−6,0).
3. 如图,方格纸中小正方形的边长均为$1$个单位长度,$A$,$B$均为格点。
(1) 在图中建立平面直角坐标系,使点$A$,$B$的坐标分别为$(3,3)$和$(-1,0)$;
(2) 在(1)中建立的坐标系的$x$轴上是否存在点$C$,使$\triangle ABC$是以$AB$为腰的等腰三角形?若存在,请写出所有满足条件的点$C$的坐标。

(1) 在图中建立平面直角坐标系,使点$A$,$B$的坐标分别为$(3,3)$和$(-1,0)$;
(2) 在(1)中建立的坐标系的$x$轴上是否存在点$C$,使$\triangle ABC$是以$AB$为腰的等腰三角形?若存在,请写出所有满足条件的点$C$的坐标。

答案:
解:(1)如答图.

(2)存在点C,使△ABC是以AB为腰的等腰三角形.
如答图,AB=$\sqrt{3^{2} + 4^{2}}$=5.
当AB=AC时,BC=8,∴C(7,0);
当AB=BC时,BC=5,∴C(−6,0)或(4,0).
∴所有满足条件的点C的坐标为(7,0)或(4,0)或(−6,0).
解:(1)如答图.

(2)存在点C,使△ABC是以AB为腰的等腰三角形.
如答图,AB=$\sqrt{3^{2} + 4^{2}}$=5.
当AB=AC时,BC=8,∴C(7,0);
当AB=BC时,BC=5,∴C(−6,0)或(4,0).
∴所有满足条件的点C的坐标为(7,0)或(4,0)或(−6,0).