6. 某校七年级组织数学知识竞赛,共设20道选择题,各题分值相同,每题必答. 下表记录了3个参赛者的得分情况.
|参赛者|答对题数|答错题数|得分|
|A|20|0|120|
|B|19|1|112|
|C|18|2|104|
(1)观察表格数据并填空,参赛者答对1道题得
(2)若参赛者D得80分,他答对了几道题?
(3)参赛者E说他得了68分,你认为可能吗? 为什么?
|参赛者|答对题数|答错题数|得分|
|A|20|0|120|
|B|19|1|112|
|C|18|2|104|
(1)观察表格数据并填空,参赛者答对1道题得
6
分,答错1道题得-2
分;(2)若参赛者D得80分,他答对了几道题?
解:设参赛者D答对了x道题.
根据题意,得6x-2(20-x)=80,解得x=15.
答:他答对了15道题.
根据题意,得6x-2(20-x)=80,解得x=15.
答:他答对了15道题.
(3)参赛者E说他得了68分,你认为可能吗? 为什么?
解:不可能.理由:设参赛者E答对了m道题.
根据题意,得6m-2(20-m)=68,
解得$ m=\frac{27}{2} $,又m为整数,故不可能.
根据题意,得6m-2(20-m)=68,
解得$ m=\frac{27}{2} $,又m为整数,故不可能.
答案:6.(1)6 -2
(2)解:设参赛者D答对了x道题.
根据题意,得6x-2(20-x)=80,解得x=15.
答:他答对了15道题.
(3)解:不可能.理由:设参赛者E答对了m道题.
根据题意,得6m-2(20-m)=68,
解得$ m=\frac{27}{2} $,又m为整数,故不可能.
(2)解:设参赛者D答对了x道题.
根据题意,得6x-2(20-x)=80,解得x=15.
答:他答对了15道题.
(3)解:不可能.理由:设参赛者E答对了m道题.
根据题意,得6m-2(20-m)=68,
解得$ m=\frac{27}{2} $,又m为整数,故不可能.
7. (2024秋·鼓楼区期中)下面是2024年1月的月历表: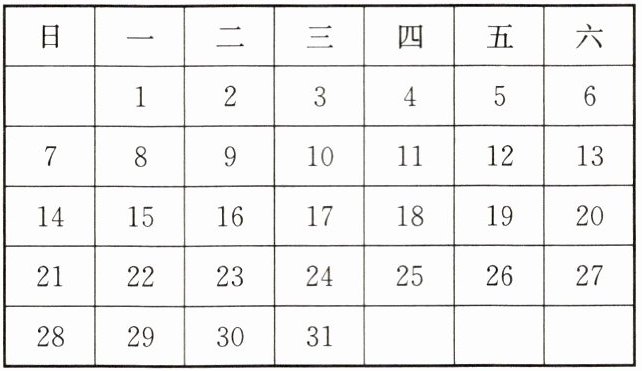
(1)在表中用优美的U形框“”框住五个数,其中最小的数为1,求U形框中的五个数 之和;
之和;
(2)在表中移动U形框的位置,若U形框框住的五个数之和为68,求这五个数中最大的数.

(1)在表中用优美的U形框“”框住五个数,其中最小的数为1,求U形框中的五个数
 之和;
之和;(2)在表中移动U形框的位置,若U形框框住的五个数之和为68,求这五个数中最大的数.
7.解:(1)根据题意得:1+3+8+10+16=38.
答:U形框中的五个数之和为38.
(2)设框住五个数中最小的数为x,则另外四个数分别为x+2,x+7,x+9,x+15.
根据题意得:x+x+2+x+7+x+9+x+15=68,
解得:x=7,则x+15=7+15=22.
答:这五个数中最大的数是22.
答:U形框中的五个数之和为38.
(2)设框住五个数中最小的数为x,则另外四个数分别为x+2,x+7,x+9,x+15.
根据题意得:x+x+2+x+7+x+9+x+15=68,
解得:x=7,则x+15=7+15=22.
答:这五个数中最大的数是22.
答案:7.解:(1)根据题意得:1+3+8+10+16=38.
答:U形框中的五个数之和为38.
(2)设框住五个数中最小的数为x,则另外四个数分别为x+2,x+7,x+9,x+15.
根据题意得:x+x+2+x+7+x+9+x+15=68,
解得:x=7,则x+15=7+15=22.
答:这五个数中最大的数是22.
答:U形框中的五个数之和为38.
(2)设框住五个数中最小的数为x,则另外四个数分别为x+2,x+7,x+9,x+15.
根据题意得:x+x+2+x+7+x+9+x+15=68,
解得:x=7,则x+15=7+15=22.
答:这五个数中最大的数是22.