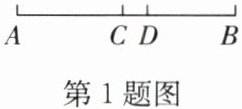
1. 如图,C 为线段 AB 的中点,点 D 在线段 BC 上,且 $ AD = 7 $,$ BD = 5 $,求 CD 的长。

答案:1.解:因为AD=7,BD=5,
所以AB=AD+BD=12.
因为C为线段AB的中点,
所以BC=$\frac{1}{2}$AB=6.
因为CD=BC−BD,
所以CD=6−5=1.
所以AB=AD+BD=12.
因为C为线段AB的中点,
所以BC=$\frac{1}{2}$AB=6.
因为CD=BC−BD,
所以CD=6−5=1.
2. 如图,C 为线段 AB 的中点,延长线段 AB 到点 D,使得 $ BD = \frac{1}{3}AB $。若 $ AD = 8 $,求线段 CD 的长。


答案:2.解:因为BD=$\frac{1}{3}$AB,
所以AD=$\frac{4}{3}$AB,
所以AB=$\frac{3}{4}$AD=$\frac{3}{4}$×8=6,
所以BD=AD−AB=8−6=2.
因为C为线段AB的中点,
所以CB=$\frac{1}{2}$AB=3,
所以CD=CB+BD=3+2=5.
所以AD=$\frac{4}{3}$AB,
所以AB=$\frac{3}{4}$AD=$\frac{3}{4}$×8=6,
所以BD=AD−AB=8−6=2.
因为C为线段AB的中点,
所以CB=$\frac{1}{2}$AB=3,
所以CD=CB+BD=3+2=5.
3. 如图,已知线段 $ AB = 12cm $,C,D 在线段 AB 上,且 $ CD = 2cm $,若 E 是线段 AC 的中点,F 是线段 BD 的中点,求线段 EF 的长度。


答案:3.解:因为E是线段AC的中点,F是线段BD的中点,所以AE=CE=$\frac{1}{2}$AC,BF=DF=$\frac{1}{2}$BD.
因为AB=12cm,CD=2cm,
所以CE+DF=$\frac{1}{2}$(AC+BD)=$\frac{1}{2}$(AB−CD)=5(cm).因为EF=CE+DF+CD,
所以EF=7cm.
因为AB=12cm,CD=2cm,
所以CE+DF=$\frac{1}{2}$(AC+BD)=$\frac{1}{2}$(AB−CD)=5(cm).因为EF=CE+DF+CD,
所以EF=7cm.
4. 如图,已知 C 为线段 AB 上一点,$ AC = 12cm $,$ CB = 8cm $,D,E 分别是线段 AC,AB 的中点。
(1) 求 AD 的长度;
(2) 求 DE 的长度;
(3) 若 M 在直线 AB 上,且 $ MB = 6cm $,求 AM 的长度。

(1) 求 AD 的长度;
(2) 求 DE 的长度;
(3) 若 M 在直线 AB 上,且 $ MB = 6cm $,求 AM 的长度。

答案:4.解:(1)由线段中点的性质,得AD=$\frac{1}{2}$AC=6cm.
(2)由线段的和差,得AB=AC+BC=12+8=20(cm),由线段中点的性质,得AE=$\frac{1}{2}$AB=10cm,
由线段的和差,得DE=AE−AD=10−6=4(cm).
(3)当点M在点B的右侧时,AM=AB+MB=20+6=26(cm);
当点M在点B的左侧时,AM=AB−MB=20−6=14(cm).
所以AM的长度为26cm或14cm.
(2)由线段的和差,得AB=AC+BC=12+8=20(cm),由线段中点的性质,得AE=$\frac{1}{2}$AB=10cm,
由线段的和差,得DE=AE−AD=10−6=4(cm).
(3)当点M在点B的右侧时,AM=AB+MB=20+6=26(cm);
当点M在点B的左侧时,AM=AB−MB=20−6=14(cm).
所以AM的长度为26cm或14cm.