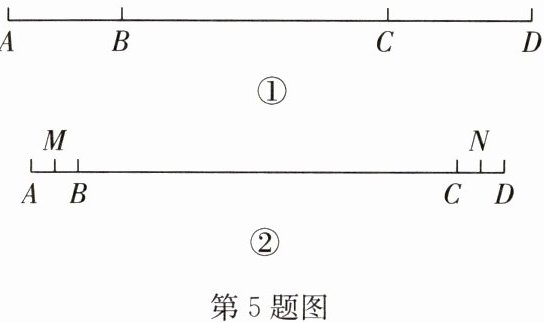
5. 如图①,已知点 B,C 在线段 AD 上。
(1) 图①中共有
(2) ①若 $ AB > CD $,比较线段的长短:$ AC $
②如图②,若 $ AD = 20 $,$ BC = 16 $,M 是线段 AB 的中点,N 是线段 CD 的中点,求线段 MN 的长度。
解:因为AD=20,BC=16,
所以AB+CD=AD−BC=4,
因为M是线段AB的中点,N是线段CD的中点,
所以BM=$\frac{1}{2}$AB,CN=$\frac{1}{2}$CD,
所以BM+CN=$\frac{1}{2}$(AB+CD)=$\frac{1}{2}$×4=2,
所以MN=BM+CN+BC=2+16=18.
(1) 图①中共有
6
条线段。(2) ①若 $ AB > CD $,比较线段的长短:$ AC $
>
$ BD $;(填“>”“=”或“<”)②如图②,若 $ AD = 20 $,$ BC = 16 $,M 是线段 AB 的中点,N 是线段 CD 的中点,求线段 MN 的长度。

解:因为AD=20,BC=16,
所以AB+CD=AD−BC=4,
因为M是线段AB的中点,N是线段CD的中点,
所以BM=$\frac{1}{2}$AB,CN=$\frac{1}{2}$CD,
所以BM+CN=$\frac{1}{2}$(AB+CD)=$\frac{1}{2}$×4=2,
所以MN=BM+CN+BC=2+16=18.
答案:5.(1)6
(2)①>
②解:因为AD=20,BC=16,
所以AB+CD=AD−BC=4,
因为M是线段AB的中点,N是线段CD的中点,
所以BM=$\frac{1}{2}$AB,CN=$\frac{1}{2}$CD,
所以BM+CN=$\frac{1}{2}$(AB+CD)=$\frac{1}{2}$×4=2,
所以MN=BM+CN+BC=2+16=18.
(2)①>
②解:因为AD=20,BC=16,
所以AB+CD=AD−BC=4,
因为M是线段AB的中点,N是线段CD的中点,
所以BM=$\frac{1}{2}$AB,CN=$\frac{1}{2}$CD,
所以BM+CN=$\frac{1}{2}$(AB+CD)=$\frac{1}{2}$×4=2,
所以MN=BM+CN+BC=2+16=18.
6. 已知线段 $ AB = 8cm $,在直线 AB 上有一点 C,且 $ AC = 4cm $,M 是线段 BC 的中点,求线段 BM 的长。
答案:6.解:①当点C在线段AB上时,BC=AB−AC=8−4=4(cm).
因为M是线段BC的中点,
所以BM=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2(cm).
②当点C在线段AB的反向延长线上时,BC=AB+AC=8+4=12(cm),
因为M是线段BC的中点,
所以BM=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6(cm).
综上,线段BM的长为2cm或6cm.
因为M是线段BC的中点,
所以BM=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2(cm).
②当点C在线段AB的反向延长线上时,BC=AB+AC=8+4=12(cm),
因为M是线段BC的中点,
所以BM=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6(cm).
综上,线段BM的长为2cm或6cm.
7. A,B,C 三点在同一条直线上,且线段 $ AB = 9cm $,M 为线段 AB 的中点,线段 $ BC = 3cm $,N 为线段 BC 的中点,求线段 MN 的长。
答案:
7.解:①当点C在线段AB上时,如答图①.
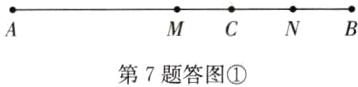
因为M为线段AB的中点,N为线段BC的中点,
所以BM=$\frac{1}{2}$AB,BN=$\frac{1}{2}$BC,
因为AB=9cm,BC=3cm,
所以BM=4.5cm,BN=1.5cm,
所以MN=BM−BN=3(cm).
②点C在线段AB的延长线上时,如答图②.

因为M为线段AB的中点,N为线段BC的中点,
所以BM=$\frac{1}{2}$AB,BN=$\frac{1}{2}$BC,
因为AB=9cm,BC=3cm,
所以BM=4.5cm,BN=1.5cm,
所以MN=BM+BN=6(cm).
综上,线段MN的长为3cm或6cm.
7.解:①当点C在线段AB上时,如答图①.

因为M为线段AB的中点,N为线段BC的中点,
所以BM=$\frac{1}{2}$AB,BN=$\frac{1}{2}$BC,
因为AB=9cm,BC=3cm,
所以BM=4.5cm,BN=1.5cm,
所以MN=BM−BN=3(cm).
②点C在线段AB的延长线上时,如答图②.

因为M为线段AB的中点,N为线段BC的中点,
所以BM=$\frac{1}{2}$AB,BN=$\frac{1}{2}$BC,
因为AB=9cm,BC=3cm,
所以BM=4.5cm,BN=1.5cm,
所以MN=BM+BN=6(cm).
综上,线段MN的长为3cm或6cm.
8. 如图,线段 $ AB = 10 $,C 为线段 AB 的延长线上一点,D 是线段 AC 的中点,且点 D 不与点 B 重合。
(1) 当 $ BC = 6 $ 时,求线段 BD 的长;
(2) 若线段 $ BD = 4 $,求线段 BC 的长。

(1) 当 $ BC = 6 $ 时,求线段 BD 的长;
(2) 若线段 $ BD = 4 $,求线段 BC 的长。

答案:
8.解:(1)因为AB=10,BC=6,
所以AC=AB+BC=16.
因为D是线段AC的中点,
所以AD=$\frac{1}{2}$AC=8,
所以BD=AB−AD=10−8=2.
(2)当点D在点B的右侧时,如答图①,AD=AB+BD=10+4=14.

因为D是线段AC的中点,
所以AD=CD=14,
所以BC=BD+CD=4+14=18.
当点D在点B的左侧时,如答图②,AD=AB−BD=10−4=6.

因为D是线段AC的中点,
所以AD=CD=6,
所以BC=CD−BD=6−4=2.
综上所述,线段BC的长为18或2.
8.解:(1)因为AB=10,BC=6,
所以AC=AB+BC=16.
因为D是线段AC的中点,
所以AD=$\frac{1}{2}$AC=8,
所以BD=AB−AD=10−8=2.
(2)当点D在点B的右侧时,如答图①,AD=AB+BD=10+4=14.

因为D是线段AC的中点,
所以AD=CD=14,
所以BC=BD+CD=4+14=18.
当点D在点B的左侧时,如答图②,AD=AB−BD=10−4=6.

因为D是线段AC的中点,
所以AD=CD=6,
所以BC=CD−BD=6−4=2.
综上所述,线段BC的长为18或2.