8. (2024春·杨浦区期末)已知点A,B,C在同一直线上,AB= 20cm,BC= $\frac{1}{3}$AC,若P为AB的中点,Q为BC的中点,则PQ= ______cm.
[答案]:
[答案]:
7.5或15
答案:7.5或15
解析:
情况1:点C在AB延长线上
设AC=x cm,则BC=$\frac{1}{3}x$ cm,
∵AC=AB+BC,∴$x=20+\frac{1}{3}x$,解得$x=30$,
∴BC=$\frac{1}{3}×30=10$ cm,
∵P为AB中点,∴PB=$\frac{1}{2}AB=10$ cm,
∵Q为BC中点,∴BQ=$\frac{1}{2}BC=5$ cm,
∴PQ=PB+BQ=10+5=15 cm.
情况2:点C在AB上
设AC=x cm,则BC=$\frac{1}{3}x$ cm,
∵AC+BC=AB,∴$x+\frac{1}{3}x=20$,解得$x=15$,
∴BC=$\frac{1}{3}×15=5$ cm,
∵P为AB中点,∴PB=$\frac{1}{2}AB=10$ cm,
∵Q为BC中点,∴BQ=$\frac{1}{2}BC=2.5$ cm,
∴PQ=PB-BQ=10-2.5=7.5 cm.
15或7.5
设AC=x cm,则BC=$\frac{1}{3}x$ cm,
∵AC=AB+BC,∴$x=20+\frac{1}{3}x$,解得$x=30$,
∴BC=$\frac{1}{3}×30=10$ cm,
∵P为AB中点,∴PB=$\frac{1}{2}AB=10$ cm,
∵Q为BC中点,∴BQ=$\frac{1}{2}BC=5$ cm,
∴PQ=PB+BQ=10+5=15 cm.
情况2:点C在AB上
设AC=x cm,则BC=$\frac{1}{3}x$ cm,
∵AC+BC=AB,∴$x+\frac{1}{3}x=20$,解得$x=15$,
∴BC=$\frac{1}{3}×15=5$ cm,
∵P为AB中点,∴PB=$\frac{1}{2}AB=10$ cm,
∵Q为BC中点,∴BQ=$\frac{1}{2}BC=2.5$ cm,
∴PQ=PB-BQ=10-2.5=7.5 cm.
15或7.5
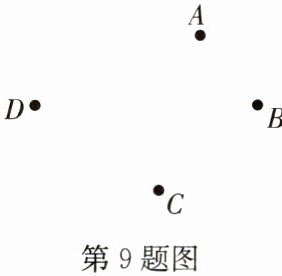
9. (14分)如图,已知四点A,B,C,D,请用尺规画图. (保留画图痕迹)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到点E,使得CE= AB+BC;
(4)在线段BD上取点P,使PA+PC的值最小.
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到点E,使得CE= AB+BC;
(4)在线段BD上取点P,使PA+PC的值最小.

答案:
解:(1)(2)(3)(4)如答图所示.
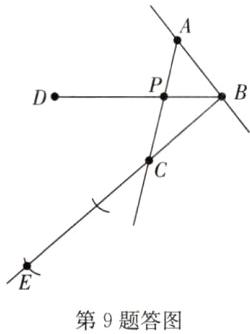
解:(1)(2)(3)(4)如答图所示.

10. (16分)如图,E是线段AB的中点,C是线段EB上一点,且EC:CB= 1:4,AC= 12cm.
(1)求AB的长;
(2)若F为线段CB的中点,求EF的长.

(1)求AB的长;
(2)若F为线段CB的中点,求EF的长.

答案:解:(1)设EC的长为x.
因为EC:CB=1:4,
所以BC=4x,
又因为BE=BC+CE,
所以BE=5x.
又因为E为线段AB的中点,
所以AE=BE=$\frac{1}{2}$AB,
所以AE=5x.
又因为AC=AE+EC,AC=12cm,
所以6x=12,解得:x=2,
所以AB=10x=20cm.
(2)在(1)的条件下,因为F为线段CB的中点,
所以CF=$\frac{1}{2}$BC=2x,
又因为EF=EC+CF,
所以EF=3x=6cm.
因为EC:CB=1:4,
所以BC=4x,
又因为BE=BC+CE,
所以BE=5x.
又因为E为线段AB的中点,
所以AE=BE=$\frac{1}{2}$AB,
所以AE=5x.
又因为AC=AE+EC,AC=12cm,
所以6x=12,解得:x=2,
所以AB=10x=20cm.
(2)在(1)的条件下,因为F为线段CB的中点,
所以CF=$\frac{1}{2}$BC=2x,
又因为EF=EC+CF,
所以EF=3x=6cm.
11. (22分)如图,C是线段AB上一点,AB= 12cm,AC= 4cm,P,Q两点分别从点A,C出发,以1cm/s,2cm/s的速度沿直线AB向右运动,运动的时间为ts.
(1)当t= 1时,CP=
(2)当运动时间为多长时,PQ= $\frac{1}{2}$AB?
(3)当运动时间为多长时,BQ= AP?
(1)当t= 1时,CP=
3
cm,QB=6
cm;(2)当运动时间为多长时,PQ= $\frac{1}{2}$AB?
解:因为AP=t,AQ=4+2t,PQ=AQ−AP,
PQ=$\frac{1}{2}$AB,所以(4+2t)−t=$\frac{1}{2}$×12,
解得t=2.
所以当运动时间为2s时,PQ=$\frac{1}{2}$AB.
PQ=$\frac{1}{2}$AB,所以(4+2t)−t=$\frac{1}{2}$×12,
解得t=2.
所以当运动时间为2s时,PQ=$\frac{1}{2}$AB.
(3)当运动时间为多长时,BQ= AP?
解:因为AP=t,BQ=|8−2t|,BQ=AP,
所以t=|8−2t|,解得t=8或t=$\frac{8}{3}$.
所以当运动时间为8s或$\frac{8}{3}$s时,BQ=AP.
所以t=|8−2t|,解得t=8或t=$\frac{8}{3}$.
所以当运动时间为8s或$\frac{8}{3}$s时,BQ=AP.
答案:(1)3 6
(2)解:因为AP=t,AQ=4+2t,PQ=AQ−AP,
PQ=$\frac{1}{2}$AB,所以(4+2t)−t=$\frac{1}{2}$×12,
解得t=2.
所以当运动时间为2s时,PQ=$\frac{1}{2}$AB.
(3)解:因为AP=t,BQ=|8−2t|,BQ=AP,
所以t=|8−2t|,解得t=8或t=$\frac{8}{3}$.
所以当运动时间为8s或$\frac{8}{3}$s时,BQ=AP.
(2)解:因为AP=t,AQ=4+2t,PQ=AQ−AP,
PQ=$\frac{1}{2}$AB,所以(4+2t)−t=$\frac{1}{2}$×12,
解得t=2.
所以当运动时间为2s时,PQ=$\frac{1}{2}$AB.
(3)解:因为AP=t,BQ=|8−2t|,BQ=AP,
所以t=|8−2t|,解得t=8或t=$\frac{8}{3}$.
所以当运动时间为8s或$\frac{8}{3}$s时,BQ=AP.