1. $0.25^{\circ}$等于(
A.$90'$
B.$60'$
C.$15'$
D.$360'$
C
)A.$90'$
B.$60'$
C.$15'$
D.$360'$
答案:C
解析:
因为$1^{\circ}=60'$,所以$0.25^{\circ}=0.25×60'=15'$。
C
C
2. 下列能用$\angle 1,\angle O,\angle MON$三种方法表示同一个角的是(
C
)答案:C
3. 下列关于角的说法:①角是由两条射线组成的图形;②角的边越长,角越大;③在角的一边延长线上取一点$D$;④角可以看作是由一条射线绕着它的端点旋转而形成的图形. 其中,正确的个数是(
A.1
B.2
C.3
D.4
A
)A.1
B.2
C.3
D.4
答案:A
解析:
①角是由公共端点的两条射线组成的图形,原说法错误;
②角的大小与边的长短无关,原说法错误;
③角的边是射线,不能延长,原说法错误;
④角可以看作是由一条射线绕着它的端点旋转而形成的图形,原说法正确。
正确的个数是1。
A
②角的大小与边的长短无关,原说法错误;
③角的边是射线,不能延长,原说法错误;
④角可以看作是由一条射线绕着它的端点旋转而形成的图形,原说法正确。
正确的个数是1。
A
4. 如图,点A在点O的正西方向,点B在点O的南偏东$30^{\circ}$方向上,若点C与点A,B在同一平面内,且点C在点O北偏东$40^{\circ}$方向上,则$\angle BOC$的度数为(
A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$150^{\circ}$
B
)A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$150^{\circ}$
答案:B
解析:
点B在点O的南偏东$30^{\circ}$方向,所以$\angle SOB = 30^{\circ}$(S表示正南方向)。
点C在点O北偏东$40^{\circ}$方向,所以$\angle NOC = 40^{\circ}$(N表示正北方向)。
因为正北与正南方向夹角为$180^{\circ}$,即$\angle NOS = 180^{\circ}$。
$\angle BOC=\angle NOS - \angle NOC - \angle SOB = 180^{\circ}-40^{\circ}-30^{\circ}=110^{\circ}$
B
点C在点O北偏东$40^{\circ}$方向,所以$\angle NOC = 40^{\circ}$(N表示正北方向)。
因为正北与正南方向夹角为$180^{\circ}$,即$\angle NOS = 180^{\circ}$。
$\angle BOC=\angle NOS - \angle NOC - \angle SOB = 180^{\circ}-40^{\circ}-30^{\circ}=110^{\circ}$
B
5. 如图,$OA是北偏东30^{\circ}$的一条射线,若$\angle AOB = 90^{\circ}$,则$OB$的方向角是
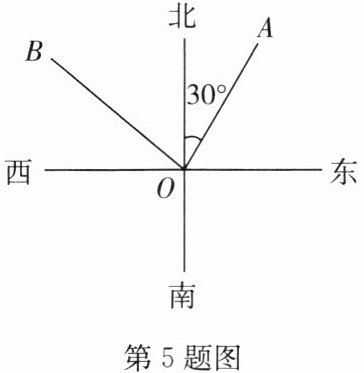
北偏西60°或西偏北30°
.
答案:北偏西60°或西偏北30°
解析:
6. 观察图形,解答下列问题.
(1)写出能用一个字母表示的角;
(2)写出以点$B$为顶点的角;
(3)图中共有几个角(小于平角)?

(1)写出能用一个字母表示的角;
(2)写出以点$B$为顶点的角;
(3)图中共有几个角(小于平角)?

答案:解:(1)能用一个字母表示的角是∠A,∠C.(2)以点B为顶点的角有∠ABD,∠ABC,∠CBD.(3)图中共有9个角.
解析:
(1)∠A,∠C.
(2)∠ABD,∠ABC,∠CBD.
(3)9个.
(2)∠ABD,∠ABC,∠CBD.
(3)9个.