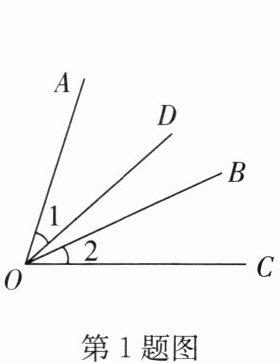
1. 如图,若$∠AOB= ∠COD$,那么 (
A.$∠1>∠2$
B.$∠1<∠2$
C.$∠1= ∠2$
D.$∠1≠∠2$
C
)
A.$∠1>∠2$
B.$∠1<∠2$
C.$∠1= ∠2$
D.$∠1≠∠2$
答案:C
解析:
由图可知,$\angle AOB = \angle 1 + \angle DOB$,$\angle COD = \angle 2 + \angle DOB$。
因为$\angle AOB = \angle COD$,所以$\angle 1 + \angle DOB = \angle 2 + \angle DOB$,等式两边同时减去$\angle DOB$,可得$\angle 1 = \angle 2$。
C
因为$\angle AOB = \angle COD$,所以$\angle 1 + \angle DOB = \angle 2 + \angle DOB$,等式两边同时减去$\angle DOB$,可得$\angle 1 = \angle 2$。
C
2. 如图,下列式子不成立的是 (
A.$∠AOC= ∠AOB+∠BOC$
B.$∠AOC= ∠AOD-∠COD$
C.$∠AOC= ∠AOB+∠BOD-∠BOC$
D.$∠AOC= ∠AOD-∠BOD+∠BOC$
C
)A.$∠AOC= ∠AOB+∠BOC$
B.$∠AOC= ∠AOD-∠COD$
C.$∠AOC= ∠AOB+∠BOD-∠BOC$
D.$∠AOC= ∠AOD-∠BOD+∠BOC$
答案:C
3. 如图,把一副三角板叠合在一起,则$∠AOB$的度数是 (
A.$15^{\circ}$
B.$20^{\circ}$
C.$30^{\circ}$
D.$70^{\circ}$
A
)A.$15^{\circ}$
B.$20^{\circ}$
C.$30^{\circ}$
D.$70^{\circ}$
答案:A
解析:
一副三角板的度数分别为:一个含$30^{\circ}$、$60^{\circ}$、$90^{\circ}$,另一个含$45^{\circ}$、$45^{\circ}$、$90^{\circ}$。由图可知,$\angle AOB$是$45^{\circ}$角与$30^{\circ}$角的差,即$\angle AOB = 45^{\circ}-30^{\circ}=15^{\circ}$。
A
A
4. 如图,点A,B,C在同一条直线上,BD平分$∠ABE$,$∠EBC= 40^{\circ}$,则$∠ABD$的度数为 (
A.$50^{\circ}$
B.$65^{\circ}$
C.$70^{\circ}$
D.$75^{\circ}$
C
)A.$50^{\circ}$
B.$65^{\circ}$
C.$70^{\circ}$
D.$75^{\circ}$
答案:C
解析:
∵点A,B,C在同一条直线上,
∴∠ABC=180°,
∵∠EBC=40°,
∴∠ABE=∠ABC - ∠EBC=180° - 40°=140°,
∵BD平分∠ABE,
∴∠ABD=∠ABE×(1/2)=140°×(1/2)=70°。
C
∴∠ABC=180°,
∵∠EBC=40°,
∴∠ABE=∠ABC - ∠EBC=180° - 40°=140°,
∵BD平分∠ABE,
∴∠ABD=∠ABE×(1/2)=140°×(1/2)=70°。
C
5. 计算:(1)$180^{\circ}-52^{\circ}18'= $
(3)$20^{\circ}45'+19^{\circ}15'= $
127°42′
; (2)$52^{\circ}45'-32^{\circ}46'= $19°59′
;(3)$20^{\circ}45'+19^{\circ}15'= $
40°
; (4)$58^{\circ}42'21''-33^{\circ}39'24''= $25°2′57″
.答案:(1)127°42′;(2)19°59′;(3)40°;(4)25°2′57″
解析:
(1)$127^{\circ}42'$;
(2)$19^{\circ}59'$;
(3)$40^{\circ}$;
(4)$25^{\circ}2'57''$
(2)$19^{\circ}59'$;
(3)$40^{\circ}$;
(4)$25^{\circ}2'57''$
6. 计算.
(1)$40^{\circ}26'+30^{\circ}30'30''÷6$; (2)$13^{\circ}53'×3-32^{\circ}5'31''$.
(1)$40^{\circ}26'+30^{\circ}30'30''÷6$; (2)$13^{\circ}53'×3-32^{\circ}5'31''$.
答案:解:(1)原式=40°26′+5°5′5″=45°31′5″.
(2)原式=41°39′-32°5′31″=9°33′29″.
(2)原式=41°39′-32°5′31″=9°33′29″.
7. 如图,$∠AOB= 150^{\circ}$,OC平分$∠AOB$,$∠AOD= 90^{\circ}$,求$∠COD$的度数.


答案:解:因为 OC 平分∠AOB,所以∠AOC=$\frac{1}{2}$∠AOB=75°,
所以∠COD=∠AOD-∠AOC=90°-75°=15°.
所以∠COD=∠AOD-∠AOC=90°-75°=15°.
8. 如图,O是直线AB上一点,OD和OE分别平分$∠AOC和∠BOC$,$∠BOC= 50^{\circ}$,则$∠AOD$的度数是 (

A.$50^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$70^{\circ}$
C
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$70^{\circ}$
答案:C
解析:
∵O是直线AB上一点,
∴∠AOB=180°,
∵∠BOC=50°,
∴∠AOC=∠AOB - ∠BOC=180° - 50°=130°,
∵OD平分∠AOC,
∴∠AOD=∠AOC×$\frac{1}{2}$=130°×$\frac{1}{2}$=65°。
C
∴∠AOB=180°,
∵∠BOC=50°,
∴∠AOC=∠AOB - ∠BOC=180° - 50°=130°,
∵OD平分∠AOC,
∴∠AOD=∠AOC×$\frac{1}{2}$=130°×$\frac{1}{2}$=65°。
C