9. 如图,OA的方向是北偏东$15^{\circ}$,OB的方向是北偏西$40^{\circ}$,若$∠AOC= ∠AOB$,则OC的方向是
北偏东 70°或东偏北 20°
.答案:北偏东 70°或东偏北 20°
解析:
∵OA的方向是北偏东$15^{\circ}$,OB的方向是北偏西$40^{\circ}$,
∴$∠AOB=40^{\circ}+15^{\circ}=55^{\circ}$。
∵$∠AOC=∠AOB=55^{\circ}$,
当OC在OA东侧时,OC与正北方向夹角为$15^{\circ}+55^{\circ}=70^{\circ}$,方向是北偏东$70^{\circ}$;
当OC在OA西侧时,OC与正北方向夹角为$15^{\circ}-55^{\circ}=-40^{\circ}$(不符合实际,舍去)。
又∵北偏东$70^{\circ}$等价于东偏北$90^{\circ}-70^{\circ}=20^{\circ}$,
∴OC的方向是北偏东$70^{\circ}$或东偏北$20^{\circ}$。
∴$∠AOB=40^{\circ}+15^{\circ}=55^{\circ}$。
∵$∠AOC=∠AOB=55^{\circ}$,
当OC在OA东侧时,OC与正北方向夹角为$15^{\circ}+55^{\circ}=70^{\circ}$,方向是北偏东$70^{\circ}$;
当OC在OA西侧时,OC与正北方向夹角为$15^{\circ}-55^{\circ}=-40^{\circ}$(不符合实际,舍去)。
又∵北偏东$70^{\circ}$等价于东偏北$90^{\circ}-70^{\circ}=20^{\circ}$,
∴OC的方向是北偏东$70^{\circ}$或东偏北$20^{\circ}$。
10. 如图,O为直线AB上一点,射线OC,OD同时从射线OA位置出发,分别以$10^{\circ}/s$,$20^{\circ}/s$的速度绕点O按逆时针方向匀速旋转,设运动的时间为$t(s)$,其中$0<t<36$.记射线OB,OC,OD中的一条射线首次平分另外两条射线组成的角的时刻为$t_{1}(s)$,射线OB,OC,OD中的一条射线最后一次平分另外两条射线组成的角的时刻为$t_{2}(s)$,则$t_{2}-t_{1}= $
24
.答案:24
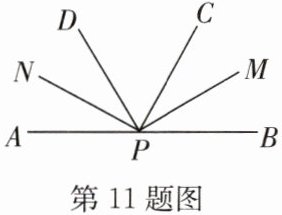
11. 如图,P为直线AB上一点,PC,PD为$∠APB$的三等分线,PM,PN分别为$∠BPC$,$∠APD$的平分线,求$∠MPN$的度数.

答案:解:因为∠APB 是平角,所以∠APB=180°.
又因为 PC,PD 为∠APB 的三等分线,
所以∠APD=∠DPC=∠BPC=$\frac{1}{3}$∠APB=60°.
又因为 PM,PN 分别为∠BPC,∠APD 的平分线,
所以∠MPC=$\frac{1}{2}$∠BPC=30°,∠NPD=$\frac{1}{2}$∠APD=30°,
所以∠MPN=∠MPC+∠CPD+∠NPD=30°+60°+30°=120°.
又因为 PC,PD 为∠APB 的三等分线,
所以∠APD=∠DPC=∠BPC=$\frac{1}{3}$∠APB=60°.
又因为 PM,PN 分别为∠BPC,∠APD 的平分线,
所以∠MPC=$\frac{1}{2}$∠BPC=30°,∠NPD=$\frac{1}{2}$∠APD=30°,
所以∠MPN=∠MPC+∠CPD+∠NPD=30°+60°+30°=120°.
12. 如图,$∠AOB$是平角,$∠AOC= 30^{\circ}$,$∠BOD= 60^{\circ}$,OM,ON分别是$∠AOC$,$∠BOD$的平分线.
(1)猜想OC与OD的位置关系,并说明理由;
(2)求$∠MON$的度数.

(1)猜想OC与OD的位置关系,并说明理由;
(2)求$∠MON$的度数.

答案:解:(1)OC⊥OD,理由如下:
∠AOC + ∠COD + ∠DOB = 180°,∠AOC = 30°,∠BOD=60°,
所以∠COD=90°,则 OC⊥OD.
(2)因为 OM 平分∠AOC,∠AOC=30°,
所以∠COM=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×30°=15°.
同理,∠DON=30°.
因为∠MON=∠COM+∠COD+∠DON,∠COD=90°,
所以∠MON=15°+90°+30°=135°.
∠AOC + ∠COD + ∠DOB = 180°,∠AOC = 30°,∠BOD=60°,
所以∠COD=90°,则 OC⊥OD.
(2)因为 OM 平分∠AOC,∠AOC=30°,
所以∠COM=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×30°=15°.
同理,∠DON=30°.
因为∠MON=∠COM+∠COD+∠DON,∠COD=90°,
所以∠MON=15°+90°+30°=135°.
13. 将一副三角板的直角顶点重合按图①方式摆放,图②是依据图①作出的几何图形,试依据图②回答下列问题:
(1)若$∠ACB= 150^{\circ}$,求$∠ACE$的度数;
(2)设$∠BCD= α$,$∠ACE= β$,试探究α,β之间的数量关系,并说明理由;
(3)请探究$∠ACB与∠DCE$之间有何数量关系?直接写出你的结论.

(1)若$∠ACB= 150^{\circ}$,求$∠ACE$的度数;
(2)设$∠BCD= α$,$∠ACE= β$,试探究α,β之间的数量关系,并说明理由;
(3)请探究$∠ACB与∠DCE$之间有何数量关系?直接写出你的结论.

答案:解:(1)因为∠BCE=90°,∠ACB=150°,
所以∠ACE=∠ACB-∠BCE=150°-90°=60°.
(2)α=β,理由如下:
因为∠BCE=∠ACD=90°,
所以∠BCE-∠DCE=∠ACD-∠DCE,
所以∠BCD=∠ACE,
所以α=β.
(3)∠ACB+∠DCE=180°.
所以∠ACE=∠ACB-∠BCE=150°-90°=60°.
(2)α=β,理由如下:
因为∠BCE=∠ACD=90°,
所以∠BCE-∠DCE=∠ACD-∠DCE,
所以∠BCD=∠ACE,
所以α=β.
(3)∠ACB+∠DCE=180°.