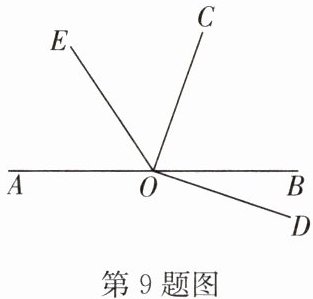
2025年启东中学作业本七年级数学上册人教版第137页解析答案

9. 如图,$∠AOC与∠BOC$互为补角,$∠BOC与∠BOD$互为余角,且$∠BOC= 4∠BOD$.
(1)求$∠BOC$的度数；
(2)若OE平分$∠AOC$,求$∠BOE$的度数.

答案：解：(1)因为∠BOC 与∠BOD 互为余角，
所以∠BOC+∠BOD=90°.
因为∠BOC=4∠BOD，
所以∠BOC=$\frac{4}{5}$×90°=72°.
(2)因为∠AOC 与∠BOC 互为补角，
所以∠AOC+∠BOC=180°，
所以∠AOC=180°-∠BOC=180°-72°=108°.
因为 OE 平分∠AOC，
所以∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×108°=54°，
所以∠BOE=∠COE+∠BOC=54°+72°=126°.

10. 如图,O是直线AB上一点,OC为任意一条射线,OD平分$∠BOC$,OE平分$∠AOC$.
(1)指出图中$∠AOD$的补角,$∠BOE$的补角；
(2)若$∠BOC= 68^{\circ }$,求$∠COD和∠EOC$的度数；
(3)$∠COD与∠EOC$具有怎样的数量关系？

答案：解：(1)∠AOD 的补角为∠BOD，∠COD；∠BOE 的补角为∠AOE，∠COE.
(2)因为 OD 平分∠BOC，∠BOC=68°，所以∠COD=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×68°=34°.
因为∠BOC=68°，所以∠AOC=180°-∠BOC=180°-68°=112°.
因为 OE 平分∠AOC，所以∠EOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×112°=56°.
(3)因为 OD 平分∠BOC，OE 平分∠AOC，
所以∠COD=$\frac{1}{2}$∠BOC，∠EOC=$\frac{1}{2}$∠AOC，
所以∠COD+∠EOC=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$×180°=90°.

11. 如图,将一个直角三角尺OAB的直角顶点O落在直线CD上,OE平分$∠AOD$.
(1)如图①,当点A,B在CD的同侧时,若$∠AOC= 58^{\circ }$,求$∠BOE$的度数；
(2)如图②,当点A,B在CD的异侧时,若$∠AOE= 2∠BOD$,求$∠AOC$的度数.

答案：解：(1)因为∠AOC=58°，∠AOB=90°，
所以∠AOD=180°-58°=122°，∠BOD=180°-58°-90°=32°.
因为 OE 平分∠AOD，
所以∠DOE=$\frac{1}{2}$∠AOD=61°，
所以∠BOE=∠DOE-∠BOD=61°-32°=29°.
(2)因为∠AOE=2∠BOD，
所以设∠BOD=α，∠AOE=2α.
因为 OE 平分∠AOD，
所以∠AOD=2∠AOE=4α.
因为∠AOB=90°，
所以α+4α=90°，解得α=18°，
所以∠AOD=4α=4×18°=72°，
所以∠AOC=180°-72°=108°.