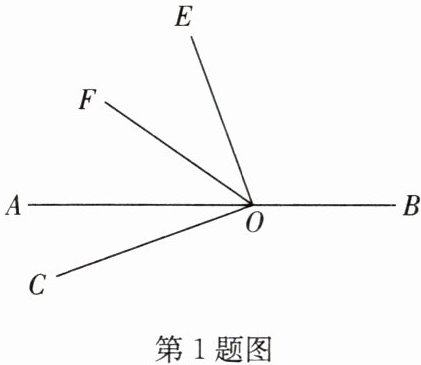
1. 如图,点 O 在直线 AB 上,$\angle COE = 90^\circ$,OF 平分$\angle AOE$。
(1) 若$\angle COF = 57^\circ$,求$\angle BOE$的度数;
(2) 若$\angle COF = \alpha$,则$\angle BOE = $______
(1) 若$\angle COF = 57^\circ$,求$\angle BOE$的度数;
(2) 若$\angle COF = \alpha$,则$\angle BOE = $______
2α
。(用含$\alpha$的式子表示)
1.(1)解:因为∠COE=90°,∠COF=57°,
所以∠EOF=90°−57°=33°.
因为OF平分∠AOE,
所以∠AOE=2∠EOF=66°,
所以∠BOE=180°−66°=114°.
(2)2α
所以∠EOF=90°−57°=33°.
因为OF平分∠AOE,
所以∠AOE=2∠EOF=66°,
所以∠BOE=180°−66°=114°.
(2)2α
答案:1.(1)解:因为∠COE=90°,∠COF=57°,
所以∠EOF=90°−57°=33°.
因为OF平分∠AOE,
所以∠AOE=2∠EOF=66°,
所以∠BOE=180°−66°=114°.
(2)2α
所以∠EOF=90°−57°=33°.
因为OF平分∠AOE,
所以∠AOE=2∠EOF=66°,
所以∠BOE=180°−66°=114°.
(2)2α
2. 如图,点 O 在直线 AB 上,已知$\angle 1 = 30^\circ$。
(1) 若$\angle COE = 90^\circ$,则$\angle 2 = $
(2) 若$\angle COE = 2\angle 2$,求$\angle 2$的度数;
(3) 在(2)的条件下,若 OD 平分$\angle BOE$,求$\angle COD$的度数。
(1) 若$\angle COE = 90^\circ$,则$\angle 2 = $
60
$^\circ$;(2) 若$\angle COE = 2\angle 2$,求$\angle 2$的度数;
解:因为∠1+∠BOE=180°,∠1=30°,
所以∠BOE=180°−∠1=180°−30°=150°,
又因为∠COE=2∠2,
所以∠BOE=3∠2,
所以∠2=$\frac{1}{3}$∠BOE=$\frac{1}{3}$×150°=50°.
所以∠BOE=180°−∠1=180°−30°=150°,
又因为∠COE=2∠2,
所以∠BOE=3∠2,
所以∠2=$\frac{1}{3}$∠BOE=$\frac{1}{3}$×150°=50°.
(3) 在(2)的条件下,若 OD 平分$\angle BOE$,求$\angle COD$的度数。
解:因为OD平分∠BOE,∠BOE=150°,
所以∠BOD=$\frac{1}{2}$∠BOE=$\frac{1}{2}$×150°=75°,
因为∠2=50°,
所以∠COD=∠BOD−∠2=75°−50°=25°.
所以∠BOD=$\frac{1}{2}$∠BOE=$\frac{1}{2}$×150°=75°,
因为∠2=50°,
所以∠COD=∠BOD−∠2=75°−50°=25°.
答案:2.(1)60
(2)解:因为∠1+∠BOE=180°,∠1=30°,
所以∠BOE=180°−∠1=180°−30°=150°,
又因为∠COE=2∠2,
所以∠BOE=3∠2,
所以∠2=$\frac{1}{3}$∠BOE=$\frac{1}{3}$×150°=50°.
(3)解:因为OD平分∠BOE,∠BOE=150°,
所以∠BOD=$\frac{1}{2}$∠BOE=$\frac{1}{2}$×150°=75°,
因为∠2=50°,
所以∠COD=∠BOD−∠2=75°−50°=25°.
(2)解:因为∠1+∠BOE=180°,∠1=30°,
所以∠BOE=180°−∠1=180°−30°=150°,
又因为∠COE=2∠2,
所以∠BOE=3∠2,
所以∠2=$\frac{1}{3}$∠BOE=$\frac{1}{3}$×150°=50°.
(3)解:因为OD平分∠BOE,∠BOE=150°,
所以∠BOD=$\frac{1}{2}$∠BOE=$\frac{1}{2}$×150°=75°,
因为∠2=50°,
所以∠COD=∠BOD−∠2=75°−50°=25°.
3. 如图,点 O 在直线 AB 上,OD,OE 分别是$\angle AOC$,$\angle BOC$的平分线。
(1) 若$\angle BOC = 72^\circ 20'$,求$\angle 1$,$\angle 2$,$\angle DOE$的度数;
(2) 若$\angle BOC = \alpha$,求$\angle DOE$的度数。

(1) 若$\angle BOC = 72^\circ 20'$,求$\angle 1$,$\angle 2$,$\angle DOE$的度数;
(2) 若$\angle BOC = \alpha$,求$\angle DOE$的度数。

答案:3.解:(1)因为OD,OE分别是∠AOC,∠BOC的平分线,所以∠1=∠BOE=$\frac{1}{2}$∠BOC=36°10′,
∠2=∠AOD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(180°−∠BOC)=$\frac{1}{2}$×(180°−72°20′)=53°50′,
所以∠DOE=∠1+∠2=36°10'+53°50'=90°.
(2)因为OD,OE分别是∠AOC,∠BOC的平分线,
所以∠DOE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$×180°=90°.
∠2=∠AOD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(180°−∠BOC)=$\frac{1}{2}$×(180°−72°20′)=53°50′,
所以∠DOE=∠1+∠2=36°10'+53°50'=90°.
(2)因为OD,OE分别是∠AOC,∠BOC的平分线,
所以∠DOE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$×180°=90°.