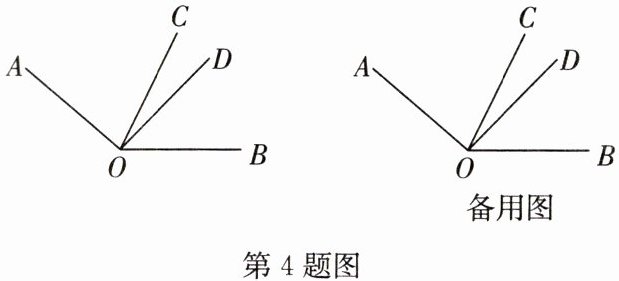
4. 如图,已知$\angle COD在\angle AOB$的内部。
(1) 若 OM,ON 分别平分$\angle AOC$,$\angle BOD$,试说明$\angle MON = \frac{1}{2}(\angle AOB + \angle COD)$;
(2) 若 OM,ON 分别平分$\angle AOD$,$\angle BOC$,试探究$\angle MON$,$\angle AOB$,$\angle COD$之间的数量关系。
(1) 若 OM,ON 分别平分$\angle AOC$,$\angle BOD$,试说明$\angle MON = \frac{1}{2}(\angle AOB + \angle COD)$;
(2) 若 OM,ON 分别平分$\angle AOD$,$\angle BOC$,试探究$\angle MON$,$\angle AOB$,$\angle COD$之间的数量关系。

答案:4.解:(1)∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=$\frac{1}{2}$∠AOC,∠DON=$\frac{1}{2}$∠BOD.
∴∠MON=∠COM+∠COD+∠DON
=$\frac{1}{2}$(∠AOC+∠BOD)+∠COD
=$\frac{1}{2}$(∠AOB−∠COD)+∠COD
=$\frac{1}{2}$(∠AOB+∠COD).
(2)∵OM平分∠AOD,ON平分∠BOC,
∴∠DOM=$\frac{1}{2}$∠AOD,∠CON=$\frac{1}{2}$∠BOC.
∴∠MON=∠DOM+∠CON−∠COD
=$\frac{1}{2}$(∠AOD+∠BOC)−∠COD
=$\frac{1}{2}$(∠AOB+∠COD)−∠COD
=$\frac{1}{2}$(∠AOB−∠COD).
∴∠COM=$\frac{1}{2}$∠AOC,∠DON=$\frac{1}{2}$∠BOD.
∴∠MON=∠COM+∠COD+∠DON
=$\frac{1}{2}$(∠AOC+∠BOD)+∠COD
=$\frac{1}{2}$(∠AOB−∠COD)+∠COD
=$\frac{1}{2}$(∠AOB+∠COD).
(2)∵OM平分∠AOD,ON平分∠BOC,
∴∠DOM=$\frac{1}{2}$∠AOD,∠CON=$\frac{1}{2}$∠BOC.
∴∠MON=∠DOM+∠CON−∠COD
=$\frac{1}{2}$(∠AOD+∠BOC)−∠COD
=$\frac{1}{2}$(∠AOB+∠COD)−∠COD
=$\frac{1}{2}$(∠AOB−∠COD).
5. 如图,已知 O 为直线 AD 上一点,OB 是$\angle AOC内部的一条射线且满足\angle AOB与\angle AOC$互补,OM,ON 分别为$\angle AOC$,$\angle AOB$的平分线。
(1) $\angle COD与\angle AOB$相等吗?请说明理由;
(2) 若$\angle AOB = 30^\circ$,求$\angle MON$的度数;
(3) 若$\angle MON = \alpha$,求$\angle AOC$的度数。(用含$\alpha$的式子表示)

(1) $\angle COD与\angle AOB$相等吗?请说明理由;
(2) 若$\angle AOB = 30^\circ$,求$\angle MON$的度数;
(3) 若$\angle MON = \alpha$,求$\angle AOC$的度数。(用含$\alpha$的式子表示)

答案:5.解:(1)相等.理由如下:
∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∵∠AOC+∠COD=180°,
∴∠COD=∠AOB.
(2)∵∠AOB与∠AOC互补,∠AOB=30°,
∴∠AOC=180°−30°=150°.
∵OM为∠AOC的平分线,
∴∠AOM=75°.
∵ON为∠AOB的平分线,
∴∠AON=15°,
∴∠MON=∠AOM−∠AON=75°−15°=60°.
(3)∵∠MON=α,
∴∠AOM−∠AON=α,
∴$\frac{1}{2}$∠AOC−$\frac{1}{2}$∠AOB=α,
∴∠AOC−∠AOB=2α,
∴∠AOC−(180°−∠AOC)=2α,
∴2∠AOC=180°+2α,
∴∠AOC=90°+α.
∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∵∠AOC+∠COD=180°,
∴∠COD=∠AOB.
(2)∵∠AOB与∠AOC互补,∠AOB=30°,
∴∠AOC=180°−30°=150°.
∵OM为∠AOC的平分线,
∴∠AOM=75°.
∵ON为∠AOB的平分线,
∴∠AON=15°,
∴∠MON=∠AOM−∠AON=75°−15°=60°.
(3)∵∠MON=α,
∴∠AOM−∠AON=α,
∴$\frac{1}{2}$∠AOC−$\frac{1}{2}$∠AOB=α,
∴∠AOC−∠AOB=2α,
∴∠AOC−(180°−∠AOC)=2α,
∴2∠AOC=180°+2α,
∴∠AOC=90°+α.
6. 如图①,在$\angle AOB$的内部画射线 OC,射线 OC 把$\angle AOB$分成两个角,分别为$\angle AOC和\angle BOC$,若这两个角中有一个角是另外一个角的 2 倍,则称射线 OC 为$\angle AOB$的“3 等分线”。
(1) 若$\angle AOB = 90^\circ$,射线 OC 为$\angle AOB$的“3 等分线”,则$\angle AOC$的度数为______;
(2) 如图②,$\angle AOB = 60^\circ$,过点 O 在$\angle AOB$外部作射线 OP,若 OA,OP,OB 三条射线中,一条射线恰好是以另外两条射线为边的角的“3 等分线”,求$\angle AOP(\angle AOP \leq 180^\circ)$的度数。

(1) 若$\angle AOB = 90^\circ$,射线 OC 为$\angle AOB$的“3 等分线”,则$\angle AOC$的度数为______;
(2) 如图②,$\angle AOB = 60^\circ$,过点 O 在$\angle AOB$外部作射线 OP,若 OA,OP,OB 三条射线中,一条射线恰好是以另外两条射线为边的角的“3 等分线”,求$\angle AOP(\angle AOP \leq 180^\circ)$的度数。

答案:
6.(1)30°或60°
(2)解:①当OA在∠BOP的内部时,如答图①.
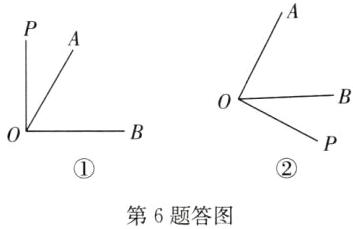
根据“3等分线”的定义可得∠AOP=$\frac{1}{2}$∠AOB=30°或∠AOP=2∠AOB=120°.
②当OB在∠AOP的内部时,如答图②.
根据“3等分线”的定义可得∠BOP=$\frac{1}{2}$∠AOB=30°或∠BOP=2∠AOB=120°,
此时∠AOP=30°+60°=90°或∠AOP=120°+60°=180°.
综上所述,∠AOP的度数是30°或90°或120°或180°.
6.(1)30°或60°
(2)解:①当OA在∠BOP的内部时,如答图①.

根据“3等分线”的定义可得∠AOP=$\frac{1}{2}$∠AOB=30°或∠AOP=2∠AOB=120°.
②当OB在∠AOP的内部时,如答图②.
根据“3等分线”的定义可得∠BOP=$\frac{1}{2}$∠AOB=30°或∠BOP=2∠AOB=120°,
此时∠AOP=30°+60°=90°或∠AOP=120°+60°=180°.
综上所述,∠AOP的度数是30°或90°或120°或180°.