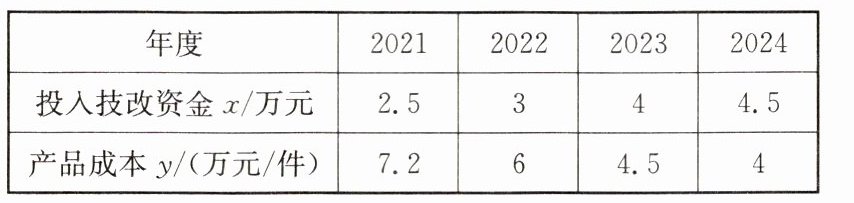
10. 某厂从2021年开始投入技改资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
请你认真分析表中数据,解决下列问题:
(1)产品成本是怎么样随着投入技改资金变化而变化的?
(2)用式子表示$y与x$的关系,$y与x$成什么关系?
请你认真分析表中数据,解决下列问题:

(1)产品成本是怎么样随着投入技改资金变化而变化的?
(2)用式子表示$y与x$的关系,$y与x$成什么关系?
答案:(1)产品成本随着投入技改资金的增加而减少.
(2)因为$2.5×7.2=3×6=4×4.5=4.5×4=18$,
所以$xy=18$,即$y=\frac{18}{x}$,
所以y与x成反比例关系.
(2)因为$2.5×7.2=3×6=4×4.5=4.5×4=18$,
所以$xy=18$,即$y=\frac{18}{x}$,
所以y与x成反比例关系.
11. 为寻求合适的销售价格,商场对新进的一种商品进行了一周的试销,发现这种商品每天的销售量$y$(千克)与销售价格$x$(元/千克)之间成反比例关系.已知第一天以220元/千克的价格销售了80千克.
(1)用式子表示$y与x$的关系;
(2)每天的销售量$y$(千克)如何随着销售价格$x$(元/千克)变化的?
(1)用式子表示$y与x$的关系;
(2)每天的销售量$y$(千克)如何随着销售价格$x$(元/千克)变化的?
答案:(1)由题意可设$y=\frac{k}{x}$.
因为第一天以220元/千克的价格销售了80千克,
所以$k=220×80=17600$,
所以y与x的关系式为$y=\frac{17600}{x}$.
(2)每天的销售量y(千克)随着销售价格x(元/千克)的增大而减小.
因为第一天以220元/千克的价格销售了80千克,
所以$k=220×80=17600$,
所以y与x的关系式为$y=\frac{17600}{x}$.
(2)每天的销售量y(千克)随着销售价格x(元/千克)的增大而减小.
12. 一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,经过6小时可达乙地.
(1)甲、乙两地相距多远?
(2)若汽车的平均速度为$v$千米/时,汽车行驶的时间为$t$小时.
①用式子表示$v与t$的关系,$v与t$成什么关系?
②如果汽车的平均速度$v$提高,那么从甲地到乙地所需的时间将怎样变化?
(1)甲、乙两地相距多远?
(2)若汽车的平均速度为$v$千米/时,汽车行驶的时间为$t$小时.
①用式子表示$v与t$的关系,$v与t$成什么关系?
②如果汽车的平均速度$v$提高,那么从甲地到乙地所需的时间将怎样变化?
答案:(1)$50×6=300$(千米).
答:甲、乙两地相距300千米.
(2)①用式子表示v与t的关系为$v=\frac{300}{t}$,v与t成反比例关系.
②如果汽车的平均速度v提高,那么从甲地到乙地所需的时间将减少.
答:甲、乙两地相距300千米.
(2)①用式子表示v与t的关系为$v=\frac{300}{t}$,v与t成反比例关系.
②如果汽车的平均速度v提高,那么从甲地到乙地所需的时间将减少.