8. 如图,某长方形广场的长为am,宽为bm,中间有一个圆形花坛,半径为cm.
(1)用整式表示图中阴影部分的面积;
(2)若$a = 100,b = 50,c = 10$,求阴影部分的面积.(π取3.14)
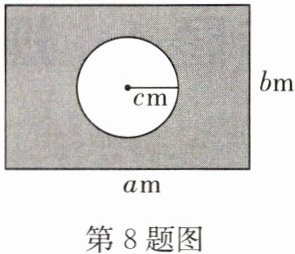
(1)用整式表示图中阴影部分的面积;
(2)若$a = 100,b = 50,c = 10$,求阴影部分的面积.(π取3.14)

答案:解:(1)$ S_{阴影}=(ab-\pi c^{2})m^{2} $.
(2)当a=100,b=50,c=10时,
$ S_{阴影}=ab-\pi c^{2}=100× 50-3.14× 10^{2}=4686(m^{2}) $.
(2)当a=100,b=50,c=10时,
$ S_{阴影}=ab-\pi c^{2}=100× 50-3.14× 10^{2}=4686(m^{2}) $.
9. 小芳房间窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同),已知长方形窗户的长为a,宽为b.
(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光的面积是多少?(窗框面积忽略不计)

(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光的面积是多少?(窗框面积忽略不计)

答案:解:(1)装饰物所占的面积为$ \pi (\frac{b}{4})^{2}=\frac{\pi}{16}b^{2} $.
(2)能射进阳光的面积为$ ab-\frac{\pi}{16}b^{2} $.
(2)能射进阳光的面积为$ ab-\frac{\pi}{16}b^{2} $.
10. 某窗户的形状如图所示,其中上部是半径为xcm的半圆形,下部是长为ycm的长方形.
(1)用含x,y的式子表示窗户的面积S;
(2)当$x = 40,y = 120$时,求窗户的面积S.

(1)用含x,y的式子表示窗户的面积S;
(2)当$x = 40,y = 120$时,求窗户的面积S.

答案:解:(1)由题图可得,$ S=(\frac{1}{2}\pi x^{2}+2xy)cm^{2} $.
(2)当x=40,y=120时,
$ S=\frac{1}{2}\pi× 40^{2}+2× 40× 120=(800\pi +9600)cm^{2} $.
(2)当x=40,y=120时,
$ S=\frac{1}{2}\pi× 40^{2}+2× 40× 120=(800\pi +9600)cm^{2} $.
11. (2024秋·南通期中)如图,在一块边长为a的正方形ABCD土地上,修建两个大小相同的长方形场地(图中的阴影部分).
(1)长方形场地EFNM的长$EM=$
(2)当$a = 60,b = 9$时,求阴影部分的面积.

解:当a=60,b=9时,
$ 2×(a-2b)×\frac{1}{2}(a-3b) $
=(a-2b)(a-3b)
=(60-2×9)×(60-3×9)
=42×33
=1386.
答:阴影部分的面积和是1386.
(1)长方形场地EFNM的长$EM=$
$a-2b$
,宽$EF=$$\frac{1}{2}(a-3b)$
;(均用含a,b的代数式表示)(2)当$a = 60,b = 9$时,求阴影部分的面积.

解:当a=60,b=9时,
$ 2×(a-2b)×\frac{1}{2}(a-3b) $
=(a-2b)(a-3b)
=(60-2×9)×(60-3×9)
=42×33
=1386.
答:阴影部分的面积和是1386.
答案:(1)$ a-2b $ $ \frac{1}{2}(a-3b) $
(2)解:当a=60,b=9时,
$ 2×(a-2b)×\frac{1}{2}(a-3b) $
=(a-2b)(a-3b)
=(60-2×9)×(60-3×9)
=42×33
=1386.
答:阴影部分的面积和是1386.
(2)解:当a=60,b=9时,
$ 2×(a-2b)×\frac{1}{2}(a-3b) $
=(a-2b)(a-3b)
=(60-2×9)×(60-3×9)
=42×33
=1386.
答:阴影部分的面积和是1386.