8. 若将$(x-y)$看成一个因式,则化简$(x-y)^{2}-3(x-y)-4(x-y)^{2}+5(x-y)$的结果是 (
A.$2(x-y)^{2}-3(x-y)$
B.$2(x-y)-3(x-y)^{2}$
C.$(x-y)-3(x-y)^{2}$
D.$2(x-y)^{2}-(x-y)$
B
)A.$2(x-y)^{2}-3(x-y)$
B.$2(x-y)-3(x-y)^{2}$
C.$(x-y)-3(x-y)^{2}$
D.$2(x-y)^{2}-(x-y)$
答案:B
解析:
$(x-y)^{2}-3(x-y)-4(x-y)^{2}+5(x-y)$
$=(1-4)(x-y)^{2}+(-3+5)(x-y)$
$=-3(x-y)^{2}+2(x-y)$
$=2(x-y)-3(x-y)^{2}$
B
$=(1-4)(x-y)^{2}+(-3+5)(x-y)$
$=-3(x-y)^{2}+2(x-y)$
$=2(x-y)-3(x-y)^{2}$
B
9. 若关于$x$,$y的多项式2x^{2}+3mxy-y^{2}-xy-5$化简后是二次三项式,则$m= $
$\frac{1}{3}$
.答案:$\frac{1}{3}$
解析:
$2x^{2}+3mxy - y^{2}-xy - 5=2x^{2}+(3m - 1)xy - y^{2}-5$,因为化简后是二次三项式,所以$xy$项系数为$0$,即$3m - 1=0$,解得$m=\frac{1}{3}$。
$\frac{1}{3}$
$\frac{1}{3}$
10.(2024 秋·苏州月考)若多项式$3x^{3}-6x^{2}+2x-4与多项式4x^{3}+2ax^{2}-x+5的和不含关于x$的二次项,则$a$的值是
3
.答案:3
解析:
$(3x^{3}-6x^{2}+2x-4)+(4x^{3}+2ax^{2}-x+5)$
$=3x^{3}-6x^{2}+2x-4+4x^{3}+2ax^{2}-x+5$
$=7x^{3}+(-6+2a)x^{2}+x+1$
因为和不含关于$x$的二次项,所以$-6 + 2a = 0$,解得$a = 3$。
3
$=3x^{3}-6x^{2}+2x-4+4x^{3}+2ax^{2}-x+5$
$=7x^{3}+(-6+2a)x^{2}+x+1$
因为和不含关于$x$的二次项,所以$-6 + 2a = 0$,解得$a = 3$。
3
11. 化简下列各式:
(1)$7x^{2}-5x-3+2x-6x^{2}+8$;
(2)$2a^{2}-3a-3a^{2}+5a$;
(3)$5x^{2}+x+3+4x-8x^{2}-2$;
(4)$-3x^{2}y+2x^{2}y+3xy^{2}-2xy^{2}$;
(5)$3x^{2}+2xy-4y^{2}-3xy+3y^{2}-2x^{2}$;
(6)$4ab^{2}-3a^{2}b+3ab^{2}-5a^{2}b$.
(1)$7x^{2}-5x-3+2x-6x^{2}+8$;
(2)$2a^{2}-3a-3a^{2}+5a$;
(3)$5x^{2}+x+3+4x-8x^{2}-2$;
(4)$-3x^{2}y+2x^{2}y+3xy^{2}-2xy^{2}$;
(5)$3x^{2}+2xy-4y^{2}-3xy+3y^{2}-2x^{2}$;
(6)$4ab^{2}-3a^{2}b+3ab^{2}-5a^{2}b$.
答案:解:(1)原式$=x^{2}-3x+5$. (2)原式$=(2-3)a^{2}+(-3+5)a=-a^{2}+2a$. (3)原式$=(5-8)x^{2}+(1+4)x+3-2=-3x^{2}+5x+1$. (4)原式$=(-3+2)x^{2}y+(3-2)xy^{2}=-x^{2}y+xy^{2}$. (5)原式$=(3-2)x^{2}+(2-3)xy+(-4+3)y^{2}=x^{2}-xy-y^{2}$. (6)原式$=4ab^{2}+3ab^{2}-3a^{2}b-5a^{2}b=7ab^{2}-8a^{2}b$.
12. 有这样一道题:求多项式$7a^{3}-6a^{3}b+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}+1$的值,其中$a= 99.01$,$b= -123.89$. 有一位同学把$a= 99.01抄成了a= -99.01$,$b= -123.89抄成了b= 123.89$,结果也正确. 为什么?
答案:解:$7a^{3}-6a^{3}b+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}+1$$=(7a^{3}+3a^{3}-10a^{3})+(-6a^{3}b+6a^{3}b)+(3a^{2}b-3a^{2}b)+1$$=1$. 因为这个多项式的值与$a$,$b$的值无关,所以$a$,$b$的值抄错后,答案仍然是1.
13.(2024 秋·莲湖区期中)如图,这是一套住宅的建筑平面图(单位:m).
(1)这套住宅的建筑面积为
(2)该套住宅的销售价格为每平方米 1.5 万元,当$x= 6$,$y= 4$时,求该套住宅的总价.
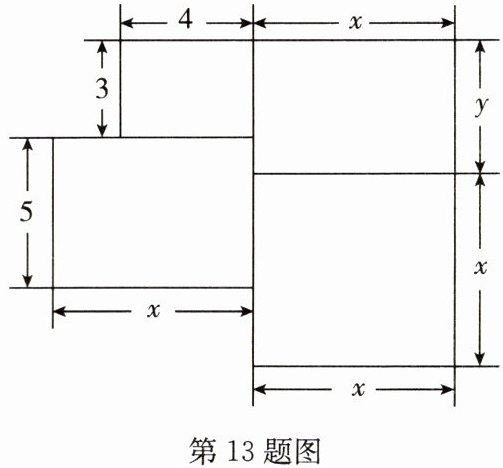
(1)这套住宅的建筑面积为
$x^{2}+xy+5x+12$
$m^{2}$;(用含$x$,$y$的代数式表示)(2)该套住宅的销售价格为每平方米 1.5 万元,当$x= 6$,$y= 4$时,求该套住宅的总价.

(2)解:当$x=6$,$y=4$时,$x^{2}+xy+5x+12=6^{2}+6×4+5×6+12=102$,1.5×102=153(万元). 答:该套住宅的总价为153万元.
答案:(1)$x^{2}+xy+5x+12$ (2)解:当$x=6$,$y=4$时,$x^{2}+xy+5x+12=6^{2}+6×4+5×6+12=102$,1.5×102=153(万元). 答:该套住宅的总价为153万元.