1.(2024秋·鼓楼区期中)比0小3的数是(
A.0
B.$-3$
C.3
D.$\pm 3$
B
)A.0
B.$-3$
C.3
D.$\pm 3$
答案:B
解析:
比0小3的数可表示为$0 - 3$,计算得$0 - 3=-3$。
答案:B
答案:B
2. 将$-3-(+6)-(-5)+(-2)$改写成省略括号和加号的形式是(
A.$-3+6-5-2$
B.$-3-6+5-2$
C.$-3-6-5-2$
D.$-3-6+5+2$
B
)A.$-3+6-5-2$
B.$-3-6+5-2$
C.$-3-6-5-2$
D.$-3-6+5+2$
答案:B
解析:
解:$-3-(+6)-(-5)+(-2)$
$=-3-6+5-2$
答案:B
$=-3-6+5-2$
答案:B
3. 下列计算正确的是(
A.$1-3= -2$
B.$-3+2= -5$
C.$3× (-2)= 6$
D.$(-4)÷ (-2)= \frac{1}{2}$
A
)A.$1-3= -2$
B.$-3+2= -5$
C.$3× (-2)= 6$
D.$(-4)÷ (-2)= \frac{1}{2}$
答案:A
解析:
A. $1 - 3 = -2$,计算正确;
B. $-3 + 2 = -1$,原计算错误;
C. $3×(-2) = -6$,原计算错误;
D. $(-4)÷(-2) = 2$,原计算错误。
答案:A
B. $-3 + 2 = -1$,原计算错误;
C. $3×(-2) = -6$,原计算错误;
D. $(-4)÷(-2) = 2$,原计算错误。
答案:A
4.(2024·广东)2024年6月6日,嫦娥六号在距离地球约384000千米上演“太空牵手”,完成月球轨道的交会对接. 数据384000用科学记数法表示为(
A.$3.84× 10^{4}$
B.$3.84× 10^{5}$
C.$3.84× 10^{6}$
D.$38.4× 10^{5}$
B
)A.$3.84× 10^{4}$
B.$3.84× 10^{5}$
C.$3.84× 10^{6}$
D.$38.4× 10^{5}$
答案:B
解析:
科学记数法的表示形式为$a×10^{n}$,其中$1\leq\vert a\vert<10$,$n$为整数。确定$n$的值时,要看把原数变成$a$时,小数点移动了多少位,$n$的值与小数点移动的位数相同。当原数绝对值$\gt1$时,$n$是正数;当原数绝对值$\lt1$时,$n$是负数。
将$384000$转变为$3.84$,小数点向左移动了$5$位,所以$n=5$,故$384000=3.84×10^{5}$。
答案:B
将$384000$转变为$3.84$,小数点向左移动了$5$位,所以$n=5$,故$384000=3.84×10^{5}$。
答案:B
5.(2024秋·珠海期中)若“$\odot$”表示一种新运算,规定:$a\odot b= a× b-a$,则$(-1)\odot (-5)$的值是(
A.$-5$
B.$-6$
C.5
D.6
D
)A.$-5$
B.$-6$
C.5
D.6
答案:D
解析:
解:根据新运算规定 $a\odot b = a×b - a$,
将 $a = -1$,$b = -5$ 代入得:
$(-1)\odot (-5) = (-1)×(-5) - (-1)$
$= 5 + 1$
$= 6$
答案:D
将 $a = -1$,$b = -5$ 代入得:
$(-1)\odot (-5) = (-1)×(-5) - (-1)$
$= 5 + 1$
$= 6$
答案:D
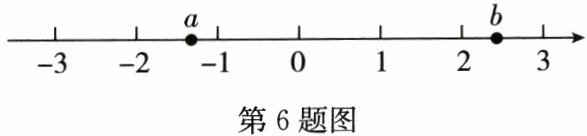
6. 有理数$a$,$b$在数轴上的位置如图所示,则下列结论正确的是(
A.$a>b$
B.$a+b>0$
C.$a-b>0$
D.$|a|>|b|$
B
) 
A.$a>b$
B.$a+b>0$
C.$a-b>0$
D.$|a|>|b|$
答案:B
解析:
由数轴可知:$-2 < a < -1$,$2 < b < 3$。
A. 因为$a$在原点左侧,$b$在原点右侧,所以$a < b$,A错误。
B. $a$的范围是$-2 < a < -1$,$b$的范围是$2 < b < 3$,则$a + b$的范围是$0 < a + b < 2$,所以$a + b > 0$,B正确。
C. $a - b = a + (-b)$,$-b$的范围是$-3 < -b < -2$,$a$的范围是$-2 < a < -1$,则$a - b$的范围是$-5 < a - b < -3$,所以$a - b < 0$,C错误。
D. $|a|$的范围是$1 < |a| < 2$,$|b|$的范围是$2 < |b| < 3$,所以$|a| < |b|$,D错误。
结论:B
A. 因为$a$在原点左侧,$b$在原点右侧,所以$a < b$,A错误。
B. $a$的范围是$-2 < a < -1$,$b$的范围是$2 < b < 3$,则$a + b$的范围是$0 < a + b < 2$,所以$a + b > 0$,B正确。
C. $a - b = a + (-b)$,$-b$的范围是$-3 < -b < -2$,$a$的范围是$-2 < a < -1$,则$a - b$的范围是$-5 < a - b < -3$,所以$a - b < 0$,C错误。
D. $|a|$的范围是$1 < |a| < 2$,$|b|$的范围是$2 < |b| < 3$,所以$|a| < |b|$,D错误。
结论:B
7. 已知$a= -3× 2^{2}$,$b= (-3× 2)^{2}$,$c= -(3× 2)^{2}$. 下列大小关系中,正确的是(
A.$a>b>c$
B.$b>c>a$
C.$b>a>c$
D.$c>a>b$
C
)A.$a>b>c$
B.$b>c>a$
C.$b>a>c$
D.$c>a>b$
答案:C
解析:
解:
计算各值:
$a = -3 × 2^2 = -3 × 4 = -12$;
$b = (-3 × 2)^2 = (-6)^2 = 36$;
$c = -(3 × 2)^2 = -6^2 = -36$。
比较大小:$36 > -12 > -36$,即$b > a > c$。
答案:C
计算各值:
$a = -3 × 2^2 = -3 × 4 = -12$;
$b = (-3 × 2)^2 = (-6)^2 = 36$;
$c = -(3 × 2)^2 = -6^2 = -36$。
比较大小:$36 > -12 > -36$,即$b > a > c$。
答案:C
8.(2024秋·句容月考)在计算$(\frac{1}{4}-\frac{5}{12}-\frac{7}{6})× (-24)$时,运用下列哪种运算律可以避免通分(
A.乘法交换律
B.乘法结合律
C.乘法分配律
D.加法结合律
C
)A.乘法交换律
B.乘法结合律
C.乘法分配律
D.加法结合律
答案:C
解析:
解:计算$(\frac{1}{4} - \frac{5}{12} - \frac{7}{6})×(-24)$时,若运用乘法分配律,可将$-24$分别与括号内的每一项相乘,即:
$\begin{aligned}&\frac{1}{4}×(-24) - \frac{5}{12}×(-24) - \frac{7}{6}×(-24)\\=&-6 + 10 + 28\end{aligned}$
此过程无需通分。而乘法交换律、乘法结合律、加法结合律均不能直接避免通分。
结论:C
$\begin{aligned}&\frac{1}{4}×(-24) - \frac{5}{12}×(-24) - \frac{7}{6}×(-24)\\=&-6 + 10 + 28\end{aligned}$
此过程无需通分。而乘法交换律、乘法结合律、加法结合律均不能直接避免通分。
结论:C
9. 小明和小红利用温差测量某山峰的高度. 小明在山顶测得的温度是$-1^{\circ}C$,小红同一时间在山脚测得的温度是$11^{\circ}C$. 已知该地区高度每增加100米,气温大约下降$0.8^{\circ}C$,则这座山峰的高度大约是(
A.800米
B.1250米
C.1200米
D.1500米
D
)A.800米
B.1250米
C.1200米
D.1500米
答案:D
解析:
解:山脚与山顶的温差为 $11 - (-1) = 12^{\circ}C$。
山峰高度为 $12 ÷ 0.8 × 100 = 1500$ 米。
答案:D
山峰高度为 $12 ÷ 0.8 × 100 = 1500$ 米。
答案:D