10.如图,一个大正方形的四个角落分别放置了四张大小不同的正方形纸片,其中1号、2号两张正方形纸片既不重叠也无空隙.已知1号正方形边长为$a$,2号正方形边长为$b$,则阴影部分的周长是(
A.$2a + 2b$
B.$4a + 2b$
C.$2a + 4b$
D.$3a + 3b$
B
)A.$2a + 2b$
B.$4a + 2b$
C.$2a + 4b$
D.$3a + 3b$
答案:B
解析:
解:设3号正方形边长为$m$,4号正方形边长为$n$。
由图可知,大正方形的边长为$a + m = b + n$,且$a - b = n - m$。
阴影部分的水平方向边长之和:$(a - b) + (b + n) + (m) + (a - m) = 2a + n$
阴影部分的竖直方向边长之和:$(b) + (n) + (m) + (a - m) = a + b + n$
又因为$a + m = b + n$,即$n = a + m - b$,代入水平方向得$2a + a + m - b = 3a + m - b$,竖直方向$a + b + a + m - b = 2a + m$。
总周长:$(3a + m - b) + (2a + m) = 5a + 2m - b$,结合$a - b = n - m$及$n = a + m - b$,化简后阴影部分周长为$4a + 2b$。
答案:B
由图可知,大正方形的边长为$a + m = b + n$,且$a - b = n - m$。
阴影部分的水平方向边长之和:$(a - b) + (b + n) + (m) + (a - m) = 2a + n$
阴影部分的竖直方向边长之和:$(b) + (n) + (m) + (a - m) = a + b + n$
又因为$a + m = b + n$,即$n = a + m - b$,代入水平方向得$2a + a + m - b = 3a + m - b$,竖直方向$a + b + a + m - b = 2a + m$。
总周长:$(3a + m - b) + (2a + m) = 5a + 2m - b$,结合$a - b = n - m$及$n = a + m - b$,化简后阴影部分周长为$4a + 2b$。
答案:B
11.用代数式表示“$m$的倒数与7的和”:
$\frac{1}{m}+7$
.答案:$\frac{1}{m}+7$
12.一种商品每件盈利$a$元,售出60件共盈利
60a
元.(用含$a$的代数式表示)答案:60a
13.一个两位数的个位数字为$m$,十位数字为$n$,则这个两位数表示为
10n+m
.答案:10n+m
14.甲数比乙数的一半少6,如果乙数为$a$,那么用含$a$的代数式表示甲数为
$\frac{1}{2}a-6$
.答案:$\frac{1}{2}a-6$
15.已知$x + y = 3$,则代数式$2x + 2y - 1$的值是
5
.答案:5
解析:
解:因为$x + y = 3$,所以$2x + 2y = 2(x + y) = 2×3 = 6$,则$2x + 2y - 1 = 6 - 1 = 5$。
5
5
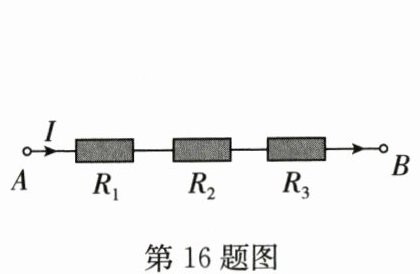
16.(2024秋·江南区月考)如图,把$R_1$,$R_2$,$R_3$三个电阻串联起来,线路$AB上的电流为I$,电压为$U$,则$U = IR_1 + IR_2 + IR_3$.当$R_1 = 19.7$,$R_2 = 32.4$,$R_3 = 35.9$,$I = 2.5$时,$U$的值为______
220
.
答案:220
解析:
解:$U = IR_1 + IR_2 + IR_3 = I(R_1 + R_2 + R_3)$
$R_1 + R_2 + R_3 = 19.7 + 32.4 + 35.9 = 88$
$U = 2.5×88 = 220$
220
$R_1 + R_2 + R_3 = 19.7 + 32.4 + 35.9 = 88$
$U = 2.5×88 = 220$
220
17.某商品原价是每件$a$元,第一次降价打九折,第二次降价每件又减50元,则第二次降价后的售价为每件
0.9a-50
元.(用含$a$的代数式表示)答案:0.9a-50
18.(2024秋·苏州月考)如图,将形状、大小完全相同的“·”和线段按照一定规律摆成图形,第1幅图中“·”的个数为$a_1$,第2幅图中“·”的个数为$a_2$,第3幅图中“·”的个数为$a_3$,以此类推,则$a_4$的值为______,$\frac{1}{a_1} + \frac{1}{a_2} + \frac{1}{a_3} + … + \frac{1}{a_{18}}$的值为______.


24
$\frac{531}{760}$
答案:24 $\frac{531}{760}$
解析:
观察图形规律:
第1幅图:$a_1=3=1×3$
第2幅图:$a_2=8=2×4$
第3幅图:$a_3=15=3×5$
可得第n幅图中“·”的个数为$a_n=n(n+2)$
则$a_4=4×(4+2)=24$
$\frac{1}{a_n}=\frac{1}{n(n+2)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$
$\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_{18}}=\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})+\cdots+(\frac{1}{18}-\frac{1}{20})]$
$=\frac{1}{2}[1+\frac{1}{2}-\frac{1}{19}-\frac{1}{20}]$
$=\frac{1}{2}[\frac{3}{2}-\frac{39}{380}]$
$=\frac{1}{2}×\frac{570 - 39}{380}$
$=\frac{1}{2}×\frac{531}{380}=\frac{531}{760}$
24;$\frac{531}{760}$
第1幅图:$a_1=3=1×3$
第2幅图:$a_2=8=2×4$
第3幅图:$a_3=15=3×5$
可得第n幅图中“·”的个数为$a_n=n(n+2)$
则$a_4=4×(4+2)=24$
$\frac{1}{a_n}=\frac{1}{n(n+2)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$
$\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_{18}}=\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})+\cdots+(\frac{1}{18}-\frac{1}{20})]$
$=\frac{1}{2}[1+\frac{1}{2}-\frac{1}{19}-\frac{1}{20}]$
$=\frac{1}{2}[\frac{3}{2}-\frac{39}{380}]$
$=\frac{1}{2}×\frac{570 - 39}{380}$
$=\frac{1}{2}×\frac{531}{380}=\frac{531}{760}$
24;$\frac{531}{760}$
19.(6分)用代数式表示:
(1)$m$的3倍与$n$的一半的和;
(2)$a与b$两数差的平方减去它们和的平方.
(1)$m$的3倍与$n$的一半的和;
(2)$a与b$两数差的平方减去它们和的平方.
答案:解:(1)$3m+\frac{1}{2}n$.
(2)$(a-b)^2-(a+b)^2$.
(2)$(a-b)^2-(a+b)^2$.