20.(6分)求下列代数式的值:
(1)当$a = - 1$,$b = - 3$时,求代数式$a^2 + 2ab + b^2$的值;
(2)当$a = - 4$,$b = 2$时,求代数式$\frac{a^2 - 2b}{a - b}$的值.
(1)当$a = - 1$,$b = - 3$时,求代数式$a^2 + 2ab + b^2$的值;
(2)当$a = - 4$,$b = 2$时,求代数式$\frac{a^2 - 2b}{a - b}$的值.
答案:解:(1)把a=-1,b=-3代入,得
$a^2+2ab+b^2=(-1)^2+2×(-1)×(-3)+(-3)^2$
=1+6+9
=16.
(2)把a=-4,b=2代入,得
$\frac{a^2-2b}{a-b}=\frac{(-4)^2-2×2}{-4-2}$
=$\frac{16-4}{-6}$
=-2.
$a^2+2ab+b^2=(-1)^2+2×(-1)×(-3)+(-3)^2$
=1+6+9
=16.
(2)把a=-4,b=2代入,得
$\frac{a^2-2b}{a-b}=\frac{(-4)^2-2×2}{-4-2}$
=$\frac{16-4}{-6}$
=-2.
21.(8分)判断下面各题中的两个量是否成反比例关系,并说明理由:
(1)一段铁路全程为1463km,某列车的平均速度$v$(km/h)与全程运行的时间$t$(h);
(2)等边三角形的周长$y与边长x$;
(3)某小区要种植一块面积为$1000m^2$的长方形草坪,草坪的长$y$(m)与宽$x$(m);
(4)工作效率$p$一定,工作总量$m与工作时间t$.
(1)一段铁路全程为1463km,某列车的平均速度$v$(km/h)与全程运行的时间$t$(h);
(2)等边三角形的周长$y与边长x$;
(3)某小区要种植一块面积为$1000m^2$的长方形草坪,草坪的长$y$(m)与宽$x$(m);
(4)工作效率$p$一定,工作总量$m与工作时间t$.
答案:解:(1)因为$v=\frac{1463}{t}$,所以v与t成反比例关系.
(2)因为y=3x,所以y与x不成反比例关系.
(3)因为$y=\frac{1000}{x}$,所以y与x成反比例关系.
(4)因为m=pt,所以m与t不成反比例关系.
(2)因为y=3x,所以y与x不成反比例关系.
(3)因为$y=\frac{1000}{x}$,所以y与x成反比例关系.
(4)因为m=pt,所以m与t不成反比例关系.
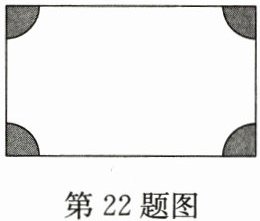
22.(8分)如图,某长方形广场的四角都有一块半径相同的扇形草地,若扇形的半径为$r$m,长方形的长为$a$m,宽为$b$m.
(1)请用代数式表示广场空地的面积;
(2)若长方形的长为300m,宽为200m,扇形的半径为10m,求广场空地的面积.
(1)请用代数式表示广场空地的面积;
(2)若长方形的长为300m,宽为200m,扇形的半径为10m,求广场空地的面积.

答案:解:(1)根据题意,长方形广场的面积为$abm^2$,
草地的面积为$4×\frac{1}{4}\pi r^2=\pi r^2(m^2)$,
所以广场空地的面积为$(ab-\pi r^2)m^2$.
(2)当a=300,b=200,r=10时,
$ab-\pi r^2=300×200-100\pi=60000-100\pi(m^2)$.
所以广场空地的面积为$(60000-100\pi)m^2$.
草地的面积为$4×\frac{1}{4}\pi r^2=\pi r^2(m^2)$,
所以广场空地的面积为$(ab-\pi r^2)m^2$.
(2)当a=300,b=200,r=10时,
$ab-\pi r^2=300×200-100\pi=60000-100\pi(m^2)$.
所以广场空地的面积为$(60000-100\pi)m^2$.
23.(8分)如图,在一个底为$a$、高为$h的三角形铁皮上剪去一个半径为r$的半圆.
(1)用含$a$,$h$,$r$的代数式表示剩下铁皮(阴影部分)的面积$S$;
(2)当$a = 8$,$h = 6$,$r = 3$时,请求出$S$的值.

(1)用含$a$,$h$,$r$的代数式表示剩下铁皮(阴影部分)的面积$S$;
(2)当$a = 8$,$h = 6$,$r = 3$时,请求出$S$的值.

答案:解:(1)$S_{阴影}=S_{三角形}-S_{半圆}=\frac{1}{2}ah-\frac{1}{2}\pi r^2$.
(2)当a=8,h=6,r=3时,
$S_{阴影}=\frac{1}{2}ah-\frac{1}{2}\pi r^2$
=$\frac{1}{2}×8×6-\frac{1}{2}\pi×3^2$
=$24-\frac{9}{2}\pi$
=$\frac{48-9\pi}{2}$.
(2)当a=8,h=6,r=3时,
$S_{阴影}=\frac{1}{2}ah-\frac{1}{2}\pi r^2$
=$\frac{1}{2}×8×6-\frac{1}{2}\pi×3^2$
=$24-\frac{9}{2}\pi$
=$\frac{48-9\pi}{2}$.