21. (4分)已知一个多项式与$x^{2}-6x的和是3x^{2}-2x+1$,求这个多项式.
答案:解:由题意知,(3x²-2x+1)-(x²-6x)=3x²-2x+1-x²+6x=2x²+4x+1.
22. (8分)(2024秋·浦东新区期中)已知$A= 2x^{2}-x+1,A-2B= -x-1$,求$B+A$,并求当$x= -1时B+A$的值.
答案:解:因为A=2x²-x+1,A-2B=-x-1,所以2x²-x+1-2B=-x-1,所以2B=2x²-x+1+x+1=2x²+2,所以B=x²+1,所以B+A=(x²+1)+(2x²-x+1)=x²+1+2x²-x+1=3x²-x+2.当x=-1时,B+A=3×(-1)²-(-1)+2=6.
解析:
解:因为$A = 2x^2 - x + 1$,$A - 2B = -x - 1$,所以$2x^2 - x + 1 - 2B = -x - 1$。
移项可得$2B = 2x^2 - x + 1 + x + 1$,化简得$2B = 2x^2 + 2$,所以$B = x^2 + 1$。
则$B + A = (x^2 + 1) + (2x^2 - x + 1)$
$= x^2 + 1 + 2x^2 - x + 1$
$= 3x^2 - x + 2$。
当$x = -1$时,$B + A = 3×(-1)^2 - (-1) + 2$
$= 3×1 + 1 + 2$
$= 3 + 1 + 2$
$= 6$。
综上,$B + A = 3x^2 - x + 2$,当$x = -1$时,$B + A$的值为$6$。
移项可得$2B = 2x^2 - x + 1 + x + 1$,化简得$2B = 2x^2 + 2$,所以$B = x^2 + 1$。
则$B + A = (x^2 + 1) + (2x^2 - x + 1)$
$= x^2 + 1 + 2x^2 - x + 1$
$= 3x^2 - x + 2$。
当$x = -1$时,$B + A = 3×(-1)^2 - (-1) + 2$
$= 3×1 + 1 + 2$
$= 3 + 1 + 2$
$= 6$。
综上,$B + A = 3x^2 - x + 2$,当$x = -1$时,$B + A$的值为$6$。
23. (8分)某同学做一道数学题:已知两个多项式A,B,$B= 2x^{2}+3x-4$,试求$A-2B$. 这位同学把$A-2B误看成A+2B$,结果求出的答案为$5x^{2}+8x-10$.
(1)请你帮这位同学求出$A-2B$的正确答案;
(2)若x是最大的负整数,求$A-2B$的值.
(1)请你帮这位同学求出$A-2B$的正确答案;
(2)若x是最大的负整数,求$A-2B$的值.
答案:解:(1)因为B=2x²+3x-4,A+2B=5x²+8x-10,所以2B=2(2x²+3x-4)=4x²+6x-8,所以A=(5x²+8x-10)-(4x²+6x-8)=5x²+8x-10-4x²-6x+8=x²+2x-2,所以A-2B=(x²+2x-2)-(4x²+6x-8)=x²+2x-2-4x²-6x+8=-3x²-4x+6.(2)因为x是最大的负整数,所以x=-1,所以A-2B=-3×(-1)²-4×(-1)+6=7.
解析:
(1)解:因为$B = 2x^{2}+3x - 4$,$A + 2B=5x^{2}+8x - 10$,所以$2B=2(2x^{2}+3x - 4)=4x^{2}+6x - 8$,则$A=(5x^{2}+8x - 10)-(4x^{2}+6x - 8)=5x^{2}+8x - 10 - 4x^{2}-6x + 8=x^{2}+2x - 2$,所以$A - 2B=(x^{2}+2x - 2)-(4x^{2}+6x - 8)=x^{2}+2x - 2 - 4x^{2}-6x + 8=-3x^{2}-4x + 6$。
(2)解:因为$x$是最大的负整数,所以$x=-1$,则$A - 2B=-3×(-1)^{2}-4×(-1)+6=-3×1 + 4 + 6=-3 + 4 + 6=7$。
(2)解:因为$x$是最大的负整数,所以$x=-1$,则$A - 2B=-3×(-1)^{2}-4×(-1)+6=-3×1 + 4 + 6=-3 + 4 + 6=7$。
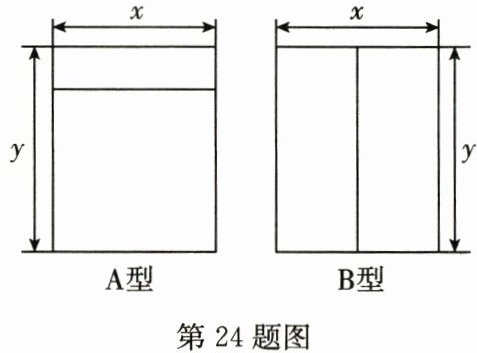
24. (8分)(2024秋·宜兴期中)如图是用相同材料做成的A,B两种造型的长方形窗框,已知窗框的长都是y米,宽都是x米$(y>x)$.
(1)若某用户需4个A型窗框,5个B型窗框,一共需要材料多少米(接缝忽略不计)?
(2)制作这两种造型的长方形窗框各一个,哪种造型更节约材料? 请说明理由.
(1)若某用户需4个A型窗框,5个B型窗框,一共需要材料多少米(接缝忽略不计)?
(2)制作这两种造型的长方形窗框各一个,哪种造型更节约材料? 请说明理由.

答案:解:(1)由题图可知,A种造型的长方形窗框有2个长,3个宽,则4个A型窗框所需材料为4×(2y+3x)=(8y+12x)米;B种造型的长方形窗框有3个长,2个宽,则5个B型窗框所需材料为5×(3y+2x)=(15y+10x)米,所以4个A型窗框和5个B型窗框一共需要材料为8y+12x+15y+10x=(22x+23y)米.(2)A种造型更节约材料.理由如下:1个A型窗框所需材料为(2y+3x)米,1个B型窗框所需材料为(3y+2x)米.(3y+2x)-(2y+3x)=y-x.因为y>x,所以y-x>0,所以(3y+2x)-(2y+3x)>0,所以3y+2x>2y+3x.
解析:
(1)由图可知,A型窗框有2个长和3个宽,所需材料为$2y + 3x$米,4个A型窗框所需材料为$4(2y + 3x)=8y + 12x$米;B型窗框有3个长和2个宽,所需材料为$3y + 2x$米,5个B型窗框所需材料为$5(3y + 2x)=15y + 10x$米。则一共需要材料:$8y + 12x + 15y + 10x=(22x + 23y)$米。
(2)A型造型更节约材料。理由如下:1个A型窗框材料为$2y + 3x$米,1个B型窗框材料为$3y + 2x$米。$(3y + 2x)-(2y + 3x)=y - x$,因为$y>x$,所以$y - x>0$,即$3y + 2x>2y + 3x$,故A型更节约材料。
(2)A型造型更节约材料。理由如下:1个A型窗框材料为$2y + 3x$米,1个B型窗框材料为$3y + 2x$米。$(3y + 2x)-(2y + 3x)=y - x$,因为$y>x$,所以$y - x>0$,即$3y + 2x>2y + 3x$,故A型更节约材料。